
【题目】已知m>0,p:(x+2)(x-6)≤0,q:2-m≤x≤2+m.
(1)若p是q成立的必要不充分条件,求实数m的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数m的取值范围.
成立的充分不必要条件,求实数m的取值范围.
【答案】(1) (0,4)(2) 实数m的取值范围为(4,+∞).
【解析】试题分析:(1)先解不等式得p,再由p是q成立的必要不充分条件得![]() ,最后根据集合包含关系以及数轴求实数m的取值范围.(2)先根据原命题与逆否命题等价得p是q的充分不必要条件,即得
,最后根据集合包含关系以及数轴求实数m的取值范围.(2)先根据原命题与逆否命题等价得p是q的充分不必要条件,即得![]() ,最后根据集合包含关系以及数轴求实数m的取值范围.
,最后根据集合包含关系以及数轴求实数m的取值范围.
试题解析:p:-2≤x≤6,
(1)∵p是q的必要不充分条件,∴[2-m,2+m] ![]() [-2,6],∴
[-2,6],∴![]() ∴m≤4.
∴m≤4.
∵当m=4时,不符合条件,∵m>0,∴m的取值范围是(0,4).
(2)∵![]() 是
是![]() 的充分不必要条件,∴p是q的充分不必要条件,
的充分不必要条件,∴p是q的充分不必要条件,
∴[-2,6]是[2-m,2+m]的真子集.
∴ 得m≥4,当m=4时,不符合条件.∴实数m的取值范围为(4,+∞).
得m≥4,当m=4时,不符合条件.∴实数m的取值范围为(4,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,AA1⊥平面ABC,AA1=2![]() ,M为A1B1的中点.
,M为A1B1的中点.
(1)求证:MC⊥AB;
(2)在棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,确定点P的位置;若不存在,说明理由.
(3)若点P为CC1的中点,求二面角B-AP-C的余弦值.
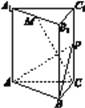
查看答案和解析>>
科目:高中数学 来源: 题型:
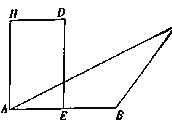
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,四边形
,四边形![]() 为矩形,固定边
为矩形,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,点
取得最小值时,点![]() 到直线
到直线![]() 的距离为__________.
的距离为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,BE=EF=FC=1,BC=2,AC=3.
,BE=EF=FC=1,BC=2,AC=3.
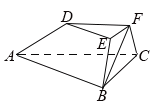
(Ⅰ)求证:EF⊥平面ACFD;
(Ⅱ)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数
为常数![]() ,对任意
,对任意![]() ,均有
,均有![]() 恒成立.下列说法:
恒成立.下列说法:
①![]() 的周期为
的周期为![]() ;
;
②若![]() 为常数)的图像关于直线
为常数)的图像关于直线![]() 对称,则
对称,则![]() ;
;
③若![]() 且
且![]() ,则必有
,则必有![]() ;
;
④已知定义在![]() 上的函数
上的函数![]() 对任意
对任意![]() 均有
均有![]() 成立,且当
成立,且当![]() 时,
时, ![]() ;又函数
;又函数![]() 为常数),若存在
为常数),若存在![]() 使得
使得![]() 成立,则
成立,则![]() 的取值范围是
的取值范围是![]() .其中说法正确的是____.(填写所有正确结论的编号)
.其中说法正确的是____.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ex-![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A. (-∞,![]() ) B. (-∞,
) B. (-∞,![]() )
)
C. (-![]() ,
, ![]() ) D. (-
) D. (-![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
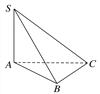
【题目】如图所示,在三棱锥S—ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=3a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1上任意一点M到直线l:y=4的距离是它到点F(0,1)距离的2倍;曲线C2是以原点为顶点,F为焦点的抛物线.
(1)求C1,C2的方程;
(2)设过点F的直线与曲线C2相交于A,B两点,分别以A,B为切点引曲线C2的两条切线l1,l2,设l1,l2相交于点P,连接PF的直线交曲线C1于C,D两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com