
已知集合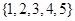 的非空子集
的非空子集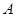 具有性质
具有性质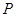 :当
:当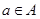 时,必有
时,必有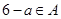 .则具有性质
.则具有性质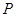 的集合
的集合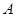 的个数是 ( )
的个数是 ( )
(A)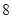 (B)
(B)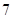 (C)
(C)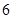 (D)
(D)
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一第一次阶段练习数学试卷(解析版) 题型:解答题
(本题满分15分)已知集合M={1,2,3,4,5},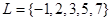 .
.
(1)用列举法表示集合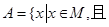
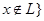 ;
;
(2)设N是M的非空真子集,且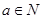 时,有
时,有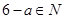 ,试写出所有集合N;
,试写出所有集合N;
(3)已知M的非空子集个数为31个,依次记为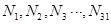 ,分别求出它们各自的元素之和,结果依次记为
,分别求出它们各自的元素之和,结果依次记为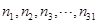 ,试计算:
,试计算: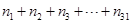 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com