
【题目】给定数列{cn},如果存在常数p、q使得cn+1=pcn+q对任意n∈N*都成立,则称{cn}为“M类数列”.
(1)若{an}是公差为d的等差数列,判断{an}是否为“M类数列”,并说明理由;
(2)若{an}是“M类数列”且满足:a1=2,an+an+1=32n.
①求a2、a3的值及{an}的通项公式;
②设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,且集合M={n|![]() ≥λ,n∈N*}中有且仅有3个元素,试求实数λ的取值范围.
≥λ,n∈N*}中有且仅有3个元素,试求实数λ的取值范围.
【答案】(1)见解析;(2)①![]() ,
,![]() ;②
;②![]()
【解析】
(1)通过an+1=an+d与cn+1=pcn+q比较可知p=1、q=d,进而可得结论;
(2)①通过a1=2、an+an+1=32n计算出a2、a3的值,进而利用数列{an}是“M类数列”代入计算可知数列{an}是以首项、公比均为2的等比数列,计算可得结论;②通过①可知2bn+22bn﹣1+23bn﹣2+…+2nb1=32n+1﹣4n﹣6,利用2bn=(2bn+22bn﹣1+23bn﹣2+…+2nb1)﹣(22bn﹣1+23bn﹣2+…+2nb1)计算可知bn=2n﹣1,从而M={n|![]() ≥λ,n∈N*},分别计算出当n=1、2、3时λ的值,进而可得结论.
≥λ,n∈N*},分别计算出当n=1、2、3时λ的值,进而可得结论.
(1)结论:公差为d的等差数列是“M类数列”.理由如下:
∵数列{an}是公差为d的等差数列,∴an+1=an+d,此时p=1、q=d,
即公差为d的等差数列是“M类数列”;
(2)①∵a1=2,an+an+1=32n,∴a2=32﹣a1=4,![]() ,
,
又∵数列{an}是“M类数列”,∴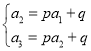 ,即
,即![]() ,解得:p=2,q=0,
,解得:p=2,q=0,
即an+1=2an,又∵a1=2,∴数列{an}是以首项、公比均为2的等比数列,
∴数列{an}的通项公式an=2n;
②由①可知a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,
即2bn+22bn﹣1+23bn﹣2+…+2nb1=32n+1﹣4n﹣6,
∴2bn﹣1+22bn﹣2+23bn﹣3+…+2n﹣1b1=32n﹣4(n﹣1)﹣6=32n﹣4n﹣2![]() ,
,
∴22bn﹣1+23bn﹣2+…+2nb1=32n+1﹣8n﹣4,
∴2bn=(2bn+22bn﹣1+23bn﹣2+…+2nb1)﹣(22bn﹣1+23bn﹣2+…+2nb1)
=(32n+1﹣4n﹣6)﹣(32n+1﹣8n﹣4)
=4n﹣2,
即bn=2n﹣1![]() ,当
,当![]() 时,
时,![]() 也符合上式,所以bn=2n﹣1.
也符合上式,所以bn=2n﹣1.
∴集合M={n|![]() ≥λ,n∈N*}={n|
≥λ,n∈N*}={n|![]() ≥λ,n∈N*},
≥λ,n∈N*},
当n=1时,λ≤![]()
![]() ;
;
当n=3时,λ≤![]() ;当n≥4时,λ≤
;当n≥4时,λ≤![]() ;
;
又∵集合M={n|![]() ≥λ,n∈N*}中有且仅有3个元素,∴
≥λ,n∈N*}中有且仅有3个元素,∴![]() ,
,
故实数λ的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图(1)是一直角墙角,![]() ,墙角的两堵墙面和地面两两互相垂直.
,墙角的两堵墙面和地面两两互相垂直.![]() 是一块长
是一块长![]() 为
为![]() 米,宽
米,宽![]() 为
为![]() 米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物.
米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物. 
(1)若按如图(1)放置,如何放置板材才能使这个直棱柱空间最大?
(2)由于墙面使用受限,![]() 面只能使用
面只能使用![]() 米,
米,![]() 面只能使用
面只能使用![]() 米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b. 
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M. 
(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(1)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 与
与![]() 均是以
均是以![]() 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的任意一点.
上的任意一点.

(1)求证:![]() :
:
(2)在平面![]() 中,是否总存在与平面
中,是否总存在与平面![]() 平行的直线?若存在,请作出图形并说明:若不存在,请说明理由.
平行的直线?若存在,请作出图形并说明:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com