
【题目】如图所示,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,
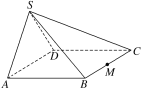
(1)求证:CD⊥平面SAD.
(2)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)见解析
【解析】
(1) 先证明CD⊥AD,再证明CD⊥平面SAD;(2)存在点N为SC的中点,连接PC,DM交于点O,连接DN,PM,SP,NM,ND,NO,先证明NO⊥平面ABCD,即证平面DMN⊥平面ABCD.
(1)证明:因为四边形ABCD为正方形,所以CD⊥AD.
又因为平面SAD⊥平面ABCD,且平面SAD∩平面ABCD=AD,
所以CD⊥平面SAD.
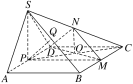
(2)存在点N为SC的中点,使得平面DMN⊥平面ABCD.
证明如下:如图,连接PC,DM交于点O,连接DN,PM,SP,NM,ND,NO,
因为PD∥CM,且PD=CM,
所以四边形PMCD为平行四边形,
所以PO=CO.
又因为点N为SC的中点,所以NO∥SP.
易知SP⊥AD,
因为平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,并且SP⊥AD,
所以SP⊥平面ABCD,
所以NO⊥平面ABCD.又因为NO平面DMN,
所以平面DMN⊥平面ABCD.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象关于点(-1,0)对称,且当x∈(-∞,0)时,
的图象关于点(-1,0)对称,且当x∈(-∞,0)时,![]() 成立,(其中f′(x)是f(x)的导数);若
成立,(其中f′(x)是f(x)的导数);若![]() ,
, ![]() ,
,![]() ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A. a>b>c B. b>a>c C. c>a>b D. c>b>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:

已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)证明:DE∥平面ABC;
(2)证明:AD⊥BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: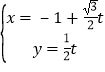 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com