
 是奇函数,(其中
是奇函数,(其中 )
)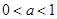 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性; 时,f(x)的值域是(1,
时,f(x)的值域是(1, ),求n与a的值。
),求n与a的值。 ;(2)
;(2) 与
与 上都是增函数;(3)
上都是增函数;(3) .
. ,由此可求出
,由此可求出 ;(2)对函数
;(2)对函数 ,判断它的单调性,应先求出定义域
,判断它的单调性,应先求出定义域 ,然后在定义域的两个区间
,然后在定义域的两个区间 与
与 上分别用单调性的定义来说明函数的单调性,这里可以先讨论对数的真数
上分别用单调性的定义来说明函数的单调性,这里可以先讨论对数的真数 的单调性,如设
的单调性,如设 ,
,
 ,判断出这个差是正数后,即得
,判断出这个差是正数后,即得 ,而由于
,而由于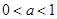 ,则有
,则有 ,于是可得函数在
,于是可得函数在 上是递增的;(3)已知条件是函数的值域是
上是递增的;(3)已知条件是函数的值域是 ,因此我们可以由值域来求自变量的取值范围,即
,因此我们可以由值域来求自变量的取值范围,即
 ,由于
,由于 ,不等式可转化为
,不等式可转化为 ,故
,故 ,这就应该是已知的范围
,这就应该是已知的范围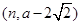 ,从而有
,从而有 ,
, ,可得结论.
,可得结论. 4分
4分 ,定义域为
,定义域为 . 5分
. 5分 上函数的单调性.
上函数的单调性. 、
、
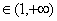 ,设
,设
 ,令
,令 ,则
,则 ,
, ,
,
 ,
,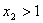 ,
,
 ,所以
,所以 ,
, ,
,
 . 7分
. 7分 时,
时, 是减函数,所以
是减函数,所以 .由定义知在
.由定义知在 上函数是增函数. 8分
上函数是增函数. 8分 是奇函数,所以在
是奇函数,所以在 上函数也是增函数. 9分
上函数也是增函数. 9分 时,要使
时,要使 的值域是
的值域是 ,则
,则 ,所以
,所以 ,即
,即 , 11分
, 11分  ,上式化为
,上式化为 ,又
,又 ,所以当
,所以当 时,
时, ;当
;当 时,
时, ; 13分
; 13分  的值域是
的值域是 ,必须
,必须 ,所以对上述不等式,当且仅当
,所以对上述不等式,当且仅当 时成立,所以
时成立,所以 解得
解得 ,
, . 18分
. 18分

科目:高中数学 来源:不详 题型:解答题
 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示,且
表示,且 (其中
(其中 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
; 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (x>0).
(x>0).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com