
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求![]() 的估计值;
的估计值;
科目:高中数学 来源: 题型:
【题目】因市场战略储备的需要,某公司![]() 月
月![]() 日起,每月
日起,每月![]() 日购买了相同金额的某种物资,连续购买了
日购买了相同金额的某种物资,连续购买了![]() 次.由于市场变化,
次.由于市场变化,![]() 月
月![]() 日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面
日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面![]() 个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )
个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )

A.①②B.①③C.②③D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
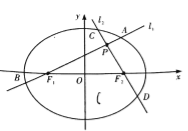
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:⑴对于定义域上的任意
同时满足:⑴对于定义域上的任意![]() ,恒有
,恒有![]() ; ⑵对于定义域上的任意
; ⑵对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中: ①
为“理想函数”.给出下列四个函数中: ①![]() ,②
,②![]() , ③
, ③![]() ,④
,④ ,能被称为“理想函数”的有_____________(填相应的序号).
,能被称为“理想函数”的有_____________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如下图).由图中数据可知a=________,估计该小学学生身高的中位数为______

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com