【答案】
分析:(Ⅰ)先求出函数的定义域,再求出其导函数,令导函数大于0得到增区间,小于0得到减区间,考虑自变量取值最后得到单调区间即可;(Ⅱ)根据(Ⅰ)求出函数的最值,不等式m<f(x)≤-m
2+2m+e
2恒成立意思是f(x)
max≤-m
2+2m+e
2,f(x)
min≥m,求出解集得到m的整数解即可;(Ⅲ)在[0,2],由f(x)=x
2+x+a和条件f(x)=x
2+2x-2ln(1+x)相等得到x
2+x+a=x
2+2x-2ln(1+x)即x-a-2ln(1+x)=0,然后令g(x)=x-a-2ln(1+x),求出其导函数,由g′(x)>0得1<x≤2;由g′(x)<0得0≤x<1.g(x)在[0,1]上单调递减,在[1,2]上单调递增.得到g(0)和g(2)都大于等于0,g(1)小于零,列出不等式组,求出解集即可a的范围.
解答:解析:(Ⅰ)由1+x>0得函数f(x)的定义域为(-1,+∞),

.
由f′(x)>0得x>0;由f′(x)<0得-1<x<0,
∴函数f(x)的递增区间是(0,+∞);递减区间是(-1,0).
(Ⅱ)由(Ⅰ)知,f(x)在
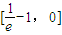
上递减,在[0,e-1]上递增.
∴f(x)
min=f(0)=0
又∵

,f(e-1)=e
2-3,且

,
∴

时,f(x)
max=e
2-3.
∵不等式m<f(x)≤-m
2+2m+e
2恒成立,
∴

,
即

∵m是整数,∴m=-1.
∴存在整数m,使不等式m<f(x)≤-m
2+2m+e
2恒成立.
(Ⅲ)由f(x)=x
2+x+a得x-a-2ln(1+x)=0,x∈[0,2]
令g(x)=x-a-2ln(1+x),则

,x∈[0,2]
由g′(x)>0得1<x≤2;由g′(x)<0得0≤x<1.
∴g(x)在[0,1]上单调递减,在[1,2]上单调递增.
∵方程f(x)=x
2+x+a在[0,2]上恰有两个相异的实根,
∴函数g(x)在[0,1)和(1,2]上各有一个零点,
∴

,
∴实数a的取值范围是1-2ln2<a≤2-2ln3
点评:考查学生利用导数研究函数单调性的能力,会求不等数恒成立的条件,以及函数与方程的综合运用能力.

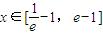 时,是否存在整数m,使不等式m<f(x)≤-m2+2m+e2恒成立?若存在,求整数m的值;若不存在,请说明理由.
时,是否存在整数m,使不等式m<f(x)≤-m2+2m+e2恒成立?若存在,求整数m的值;若不存在,请说明理由. .
.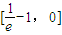 上递减,在[0,e-1]上递增.
上递减,在[0,e-1]上递增. ,f(e-1)=e2-3,且
,f(e-1)=e2-3,且 ,
, 时,f(x)max=e2-3.
时,f(x)max=e2-3. ,
,
 ,x∈[0,2]
,x∈[0,2] ,
,
