
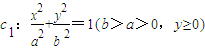 与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.
与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.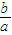 为定值时,求证k1•k2为定值(与p无关),并求出这个定值;
为定值时,求证k1•k2为定值(与p无关),并求出这个定值;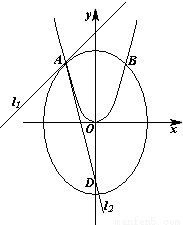
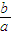 为定值时可得结论.
为定值时可得结论.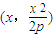 ,利用l2过点D(0,-2),则x2=4p,从而可求点
,利用l2过点D(0,-2),则x2=4p,从而可求点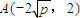 的坐标代入曲线c1的方程得
的坐标代入曲线c1的方程得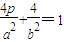 .从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.
.从而利用基本不等式可求a2+b2最小值,注意等号成立的条件.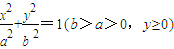 得:
得:
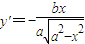 ,∴
,∴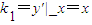 …2′
…2′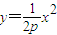 ,∴
,∴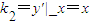 …4′
…4′
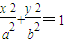 ,∴
,∴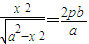 .
.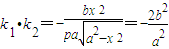 为定值.…6′
为定值.…6′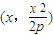 ,则x∈(-a,0).
,则x∈(-a,0).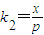 ,则直线
,则直线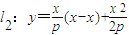 .
.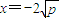 ,∴点
,∴点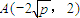 .…8′
.…8′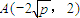 代入曲线c1的方程得
代入曲线c1的方程得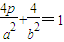 .
.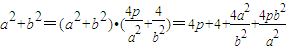 .
.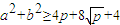 .…10′
.…10′ ,解得
,解得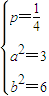
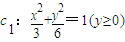 ,c2:y=2x2.…13′
,c2:y=2x2.…13′

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
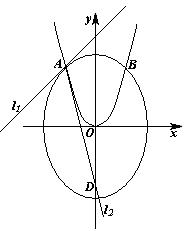
(09年湖北八校联考理)(13分)
如图,已知曲线![]() 与抛物线
与抛物线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,曲线
,曲线![]() 和抛物线
和抛物线![]() 在点
在点![]() 处的切线分别为
处的切线分别为![]() 、
、![]() ,且
,且![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .
.
(Ⅰ)当![]() 为定值时,求证
为定值时,求证![]() 为定值(与
为定值(与![]() 无关),并求出这个定值;
无关),并求出这个定值;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,当
,当![]() 取得最小值
取得最小值![]() 时,求曲线
时,求曲线![]() 和
和![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源:2013届福建省四地六校高二第一次联考理科数学 题型:解答题
(本小题满分14分)
如图,已知直线 与抛物线
与抛物线 相交于
相交于 两点,与
两点,与 轴相交于点
轴相交于点 ,若
,若 .(1)求证:
.(1)求证: 点的坐标为(1,0);(2)求△AOB的面积的最小值.
点的坐标为(1,0);(2)求△AOB的面积的最小值.

查看答案和解析>>
科目:高中数学 来源:2010年河南省信阳市新县高中高三质量调研数学试卷(理科)(解析版) 题型:解答题
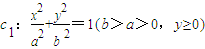 与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.
与抛物线c2:x2=2py(p>0)的交点分别为A、B,曲线c1和抛物线c2在点A处的切线分别为l1、l2,且l1、l2的斜率分别为k1、k2.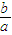 为定值时,求证k1•k2为定值(与p无关),并求出这个定值;
为定值时,求证k1•k2为定值(与p无关),并求出这个定值;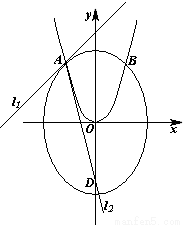
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com