
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,四边形
为顶点的五面体中,四边形![]() 为正方形,
为正方形,![]() ,
, ![]() ,
,![]() .
.

(1)证明![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明出![]() 平面
平面![]() ,然后利用线面平行的性质定理可证明出
,然后利用线面平行的性质定理可证明出![]() ,再利用空间平行线的传递性可得出结论;
,再利用空间平行线的传递性可得出结论;
(2)证明出平面![]() 平面
平面![]() ,然后作
,然后作![]() ,垂足为
,垂足为![]() ,可得出
,可得出![]() 平面
平面![]() ,由此以点
,由此以点![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长建立空间直角坐标系,利用空间向量法能求出二面角
为单位长建立空间直角坐标系,利用空间向量法能求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)![]() 四边形
四边形![]() 为正方形,
为正方形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,因此,
,因此,![]() ;
;
(![]() )
)![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
作![]() ,垂足为
,垂足为![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
以点![]() 为坐标原点,
为坐标原点,![]() 方向为
方向为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为单位长,如图建立空间直角坐标系,
为单位长,如图建立空间直角坐标系,
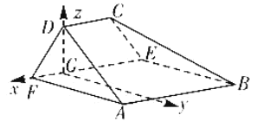
则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则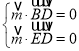 ,即
,即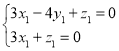 ,取
,取![]() ,则
,则![]() ,
,![]() ,所以,
,所以, ![]() ,
,
又![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 即
即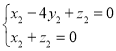 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,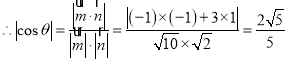 .
.
即二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到如图②所示的几何体.
,得到如图②所示的几何体.
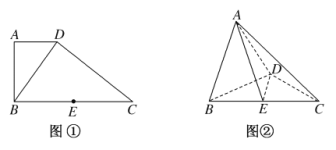
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学高三的一名学生在高考前对他在高三近一年中的所有数学考试(含模拟考试、月考、平时训练等各种类型的试卷)分数进行统计,以此来估计自己在高考中的大致分数.为此,随机抽取了若干份试卷作为样本,根据此样本数据作出如下频率分布统计表和频率分布直方图.
分组 | 频数 | 频率 |
| 20 | 0.25 |
| 50 |
|
|
|
|
| 4 | 0.05 |
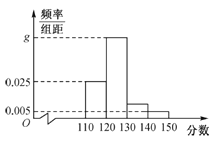
(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值;
的值;
(2)若同组中的每个数据用该组区间的中点值代替,试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数,并对该学生自己在高考中的数学成绩进行预测.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
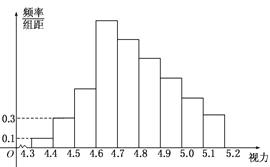
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com