
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() >0成立. (Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
>0成立. (Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
(Ⅱ)解不等式:f(2x﹣1)<f(1﹣3x);
(Ⅲ)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)任取x1 , x2∈[﹣1,1],且x1<x2 , 则﹣x2∈[﹣1,1],∵f(x)为奇函数, ∴f(x1)﹣f(x2)=f(x1)+f(﹣x2)= ![]() (x1﹣x2),…(2分)
(x1﹣x2),…(2分)
由已知得 ![]() >0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
>0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
∴f(x)在[﹣1,1]上单调递增.
(Ⅱ)∵f(x)在[﹣1,1]上单调递增,∴ 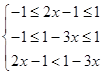
∴不等式的解集为 ![]() .
.
(Ⅲ)∵f(1)=1,f(x)在[﹣1,1]上单调递增.∴在[﹣1,1]上,f(x)≤1.
问题转化为m2﹣2am+1≥1,即m2﹣2am≥0,对a∈[﹣1,1]恒成立.
下面来求m的取值范围.设g(a)=﹣2ma+m2≥0.
①若m=0,则g(a)=0≥0,对a∈[﹣1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[﹣1,1]恒成立,
必须g(﹣1)≥0且g(1)≥0,∴m≤﹣2或m≥2.
综上,m=0 或m≤﹣2或m≥2
【解析】(Ⅰ)任取x1 , x2∈[﹣1,1],且x1<x2 , 利用函数的单调性的定义证明f(x)在[﹣1,1]上单调递增.(Ⅱ)利用f(x)在[﹣1,1]上单调递增,列出不等式组,即可求出不等式的解集.(Ⅲ)问题转化为m2﹣2am≥0,对a∈[﹣1,1]恒成立,通过①若m=0,②若m≠0,分类讨论,判断求解即可.


科目:高中数学 来源: 题型:
【题目】某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x=a0+a1×2+a2×22+a3×23},其中ai∈{0,1,2}(i=0,1,2,3),且a0≠0,则A中所有元素之和等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明家订了一份报纸,送报人可能在早上6:30﹣7:30之间把报纸送到小明家,小明父亲离开家去工作的时间在早上7:00﹣8:00之间,问小明父亲在离开家前能得到报纸(称为事件A)的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com