[题目]将函数的图像向左平移个单位后得到函数的图像.且函数满足.则下列命题中正确的是()A. 函数图像的两条相邻对称轴之间的距离为B. 函数图像关于点对称C. 函数图像关于直线对称D. 函数在区间内为单调递减函数题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】将函数的图像向左平移个单位后得到函数的图像，且函数满足，则下列命题中正确的是（）

A. 函数图像的两条相邻对称轴之间的距离为

B. 函数图像关于点对称

C. 函数图像关于直线对称

D. 函数在区间内为单调递减函数

【答案】D

【解析】

由已知可得和时函数的两条对称轴，可确定出和值，得到f(x)解析式，由平移可得函数g(x)解析式，根据正弦函数的性质对选项逐个检验判断即可得到答案.

因为函数的最大值是，所以，周期是，则又故n=1时，

又因为所以,，故

于是函数的图象向左平移个单位后得到.

函数g(x)周期为,则两条相邻对称轴之间的距离为，故选项A错误；

将代入函数g(x)解析式，函数值不为0，故选项B错误；

将代入函数g(x)解析式，函数取不到最值，故选项C错误；

当时，，由正弦函数图像可知函数单调递减，

故选：D.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

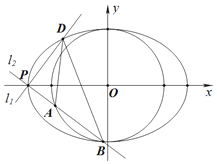
【题目】如图，已知是椭圆的一个顶点，的短轴是圆的直径，直线，过点P且互相垂直，交椭圆于另一点D，交圆于A，B两点

Ⅰ求椭圆的标准方程；

Ⅱ求面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求曲线的普通方程与曲线的直角坐标方程；

（2）若与交于两点，点的极坐标为，求的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在正三角形中，、、分别是、、边上的点，满足（如图1）.将△沿折起到的位置，使二面角成直二面角，连结、（如图2）

（Ⅰ）求证：⊥平面；

（Ⅱ）求二面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某老师是省级课题组的成员，主要研究课堂教学目标达成度，为方便研究，从实验班中随机抽取30次的随堂测试成绩进行数据分析已知学生甲的30次随堂测试成绩如下满分为100分：

把学生甲的成绩按，，，，，分成6组，列出频率分布表，并画出频率分布直方图；

规定随堂测试成绩80分以上含80分为优秀，为帮助学生甲提高成绩，选取学生乙，对甲与乙的随堂测试成绩进行对比分析，甲与乙测试成绩是否为优秀相互独立已知甲成绩优秀的概率为以频率估计概率，乙成绩优秀的概率为，若，则此二人适合为学习上互帮互助的“对子”在一次随堂测试中，记为两人中获得优秀的人数，已知，问二人是否适合结为“对子”？