练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义在R上的函数满足，且为偶函数，若在内单调递减，则下面结论正确的是（ ）

    A. B.

    C. D.

    【答案】B

    【解析】

    由题意可判断函数f（x）的周期为6，对称轴为x＝3，所以有f（12.5）＝f（0.5），f（-4.5）＝f（1.5），f（3.5）＝f（2.5），因为0＜0.5＜1.5＜2.5＜3，且函数在（0，3）内单调递减，从而判断大小

    ∵函数满足，∴=，

    ∴f（x）在R上是以6为周期的函数，∴f（12.5）＝f（12+0.5）＝f（0.5），

    又为偶函数，∴f（x）的对称轴为x＝3，∴f（3.5）＝f（2.5），

    又∵0＜0.5＜1.5＜2.5＜3，

    且在（0，3）内单调递减，∴f（2.5）＜f（1.5）＜f（0.5）

    即f（3.5）＜f（-4.5）＜f（12.5）

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= x3﹣（1+a）x2+4ax+24a，其中常数a＞1
    （1）讨论f（x）的单调性；
    （2）若当x≥0时，f（x）＞0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥P﹣ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点． （I）证明：AE⊥PD；
    （II）H是PD上的动点，EH与平面PAD所成的最大角为45°，求二面角E﹣AF﹣C的正切值．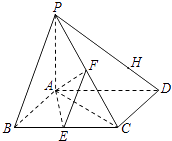

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线，，则下列结论正确的是（ ）

    A. 把上所有的点向右平移个单位长度，再把所有图象上各点的横坐标缩短到原来的倍（纵坐标不变），得到曲线

    B. 把上所有点向左平移个单位长度，再把所得图象上各点的横坐标伸长到原来的3倍（纵坐标不变），得到曲线

    C. 把上各点的横坐标缩短到原来的倍（纵坐标不变），再把所得图象上所有的点向左平移个单位长度，得到曲线

    D. 把上各点的横坐标伸长到原来的3倍（纵坐标不变），再把所得图象上所有的点向左平移个单位长度，得到曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解学生的课外阅读时间情况，某学校随机抽取了50人进行统计分析，把这50人每天阅读的时间（单位：分钟）绘制成频数分布表，如下表所示：

    阅读时间

    [0,20）

    [20,40）

    [40,60）

    [60,80）

    [80,100）

    [100,120]

    人数

    8

    10

    12

    11

    7

    2

    若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作出如图所示的等高条形图：

    （1）根据已知条件完成2x2列联表;

    男生

    女生

    总计

    阅读达人

    非阅读达人

    总计

    （2）并判断是否有的把握认为“阅读达人”跟性别有关？

    附：参考公式

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我市大学生创业孵化基地某公司生产一种“儒风邹城”特色的旅游商品.该公司年固定成本为10万元，每生产千件需另投入2.7万元；设该公司年内共生产该旅游商品千件并全部销售完，每千件的销售收入为万元，且满足函数关系：.

    （Ⅰ）写出年利润（万元）关于该旅游商品（千件）的函数解析式；

    （Ⅱ）年产量为多少千件时，该公司在该旅游商品的生产中所获年利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，f（x）=|x﹣a|
    （Ⅰ）当a=2，解不等式，f（x）≥5﹣|x﹣1|；
    （Ⅱ）若f（x）≤1的解集为[0，2]，+=a（m＞0，n＞0），求证：m+2n≥4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，是偶函数．

    （1）求的值；

    （2）若函数的图象在直线上方，求的取值范围；

    （3）若函数，，是否存在实数使得的最小值为0？若存在，求出的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对任意等比数列{an}，下列说法一定正确的是（ ）
    A.a1 ， a3 ， a9成等比数列
    B.a2 ， a3 ， a6成等比数列
    C.a2 ， a4 ， a8成等比数列
    D.a3 ， a6 ， a9成等比数列

    查看答案和解析>>

    同步练习册答案