
在空间四边形 中,
中,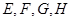 分别是
分别是 的中点。若
的中点。若 ,且
,且 与
与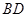 所成的角为
所成的角为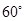 ,则四边形
,则四边形 的面积为( )
的面积为( )
A. | B. | C. | D.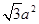 |
A
解析试题分析:连接EH,因为EH是△ABD的中位线,所以EH∥BD,且EH=BD.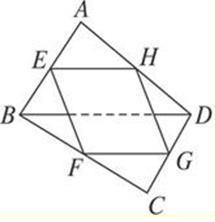
同理,FG∥BD,EF∥AC,且FG=BD,EF=AC.
所以EH∥FG,且EH=FG.
所以四边形EFGH为平行四边形.
因为AC=BD=a,AC与BD所成的角为60°
所以EF=EH.所以四边形EFGH为菱形,∠EFG=60°.
∴四边形EFGH的面积是2×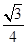 ×(
×(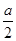 )2=
)2=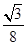 a2
a2
故答案为: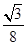 a2选A.
a2选A.
考点:本题主要是考查的知识点简单几何体和公理四,公理四:和同一条直线平行的直线平行,证明菱形常用方法是先证明它是平行四边形再证明邻边相等相等,以及面积公式属于基础题.
点评:解决该试题的关键是先证明四边形EFGH为菱形,然后说明∠EFG=60°,最后根据三角形的面积公式即可求出所求.


科目:高中数学 来源: 题型:单选题
一个盛满水的三棱锥容器,如图所示,不久发现三个侧棱上各有一个小洞D,E,F。且知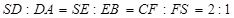 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )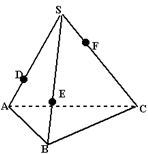
A.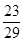 | B.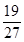 | C.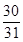 | D.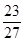 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的棱锥体积最大时,直线BD和平面ABC所成的角的大小为 ( )
A. 90° B .60° C . 45° D .30°
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设四棱锥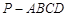 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面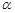 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面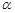 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com