
【题目】已知函数f(x)是奇函数,当x<0,f(x)=﹣x2+x,若不等式f(x)﹣x≤2logax(a>0且a≠1)对x∈(0, ![]() ]恒成立,则实数a的取值范围是( )
]恒成立,则实数a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,1)
,1)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() ]∪(1,+∞)
]∪(1,+∞)
【答案】B
【解析】解:函数f(x)是奇函数,当x<0,f(x)=﹣x2+x ∴f(﹣x)=﹣f(x),
设x>0,则﹣x<0,
∴f(﹣x)=﹣x2﹣x,
∴f(x)=x2+x,
∵不等式f(x)﹣x≤2logax(a>0,a≠1)对x∈(0, ![]() ]恒成立,
]恒成立,
∴x2+x﹣x≤2logax(a>0,a≠1)对x∈(0, ![]() ]恒成立,
]恒成立,
∴x2≤logax2 ,
∴( ![]() )2≤loga(
)2≤loga( ![]() )2 ,
)2 ,
∴loga ![]() =
= ![]() ≤loga
≤loga ![]() ,
,
当a>1时, ![]() ≤
≤ ![]() ,解得a≤
,解得a≤ ![]() ,此时无解,
,此时无解,
当0<a<1时, ![]() ≥
≥ ![]() ,解得a≥
,解得a≥ ![]() ,此时
,此时 ![]() ≤a<1,
≤a<1,
综上所述a的取值范围为[ ![]() ,1).
,1).
故选:B.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】定义f(x)={x}(其中{x}表示不小于x的最小整数)为“取上整函数”,例如{2.1}=3,{4}=4.以下关于“取上整函数”性质的描述,正确的是( ) ①f(2x)=2f(x);
②若f(x1)=f(x2),则x1﹣x2<1;
③任意x1 , x2∈R,f(x1+x2)≤f(x1)+f(x2);
④ ![]() .
.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2. 
(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)若二面角B﹣AB1﹣C1的余弦值为 ![]() ,求斜三棱柱ABC﹣A1B1C1的高.
,求斜三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即S= ![]() ,现有周长为10+2
,现有周长为10+2 ![]() 的△ABC满足sinA:sinB:sinC=2:3:
的△ABC满足sinA:sinB:sinC=2:3: ![]() ,则用以上给出的公式求得△ABC的面积为( )
,则用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为 ![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若 ![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线l过右焦点 ![]() (不与x轴重合)且与椭圆相交于不同的两点A,B,在x轴上是否存在一个定点P(x0 , 0),使得
(不与x轴重合)且与椭圆相交于不同的两点A,B,在x轴上是否存在一个定点P(x0 , 0),使得 ![]() 的值为定值?若存在,写出P点的坐标(不必求出定值);若不存在,说明理由.
的值为定值?若存在,写出P点的坐标(不必求出定值);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax+lnx,a∈R.
(1)当a=3时,求函数f(x)的极小值;
(2)令g(x)=x2﹣f(x),是否存在实数a,当x∈[1,e](e是自然对数的底数)时,函数g(x)取得最小值为1.若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手.从这7名队员中随机选派4名队员参加第一阶段的比赛.
(1)求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
(2)设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 . 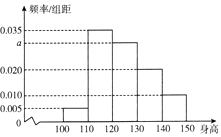
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程选讲]
在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1 , C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)求C1和C2交点的极坐标;
(Ⅱ)直线l的参数方程为:  (t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com