
【题目】已知等比数列{an}满足2a1+a3=3a2 , 且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=an+log2 ![]() ,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
【答案】
(1)解:设等比数列{an}的首项为a1,公比为q,
依题意,∵2a1+a3=3a2,且a3+2是a2,a4的等差中项
∴ 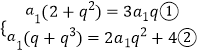
由 ①得 q2﹣3q+2=0,解得q=1或q=2.
当q=1时,不合题意舍;
当q=2时,代入(2)得a1=2,所以an=2n.
(2)解: ![]() =2n﹣n
=2n﹣n
所以Sn=b1+b2+…bn=(2+22++2n)﹣(1+2+…+n)=2n+1﹣2﹣ ![]() ﹣
﹣ ![]() n2
n2
因为 ![]() ,所以2n+1﹣2﹣
,所以2n+1﹣2﹣ ![]() ﹣
﹣ ![]() n2﹣2n+1+47<0,
n2﹣2n+1+47<0,
即n2+n﹣90>0,解得n>9或n<﹣10.
故使 ![]() 成立的正整数n的最小值为10
成立的正整数n的最小值为10
【解析】(1)设等比数列{an}的首项为a1 , 公比为q,根据2a1+a3=3a2 , 且a3+2是a2 , a4的等差中项,建立方程组,从而可求数列{an}的通项公式;(2) ![]() =2n﹣n,求出Sn=b1+b2+…bn , 再利用
=2n﹣n,求出Sn=b1+b2+…bn , 再利用 ![]() ,建立不等式,即可求得使
,建立不等式,即可求得使 ![]() 成立的正整数n的最小值.
成立的正整数n的最小值.
【考点精析】掌握等比数列的通项公式(及其变式)是解答本题的根本,需要知道通项公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分10分) 选修4-4:极坐标系与参数方程
在极坐标系中曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() .以极点
.以极点![]() 为原点,以极轴为
为原点,以极轴为![]() 轴正半轴建立直角坐标系.斜率为
轴正半轴建立直角坐标系.斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)求点![]() 到两点
到两点![]() 的距离之积.
的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,边a、b、c分别是角A、B、C的对边,且满足bcosC=(3a﹣c)cosB.
(1)求cosB;
(2)若 ![]()
![]() =4,b=4
=4,b=4 ![]() ,求边a,c的值.
,求边a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别是a,b,c,a=2,且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设锐角△ABC的三内角A、B、C所对边的边长分别为a、b、c,且 a=1,B=2A,则b的取值范围为( )
A.( ![]() ,
, ![]() )
)
B.(1, ![]() )
)
C.( ![]() ,2)
,2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=asin(2x+ ![]() )+b
)+b
(1)若a>0,求f(x)的单调递增区间;
(2)当x∈[0, ![]() ]时,f(x)的值域为[1,3],求a,b的值.
]时,f(x)的值域为[1,3],求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com