空间四边形ABCD中,AC与BD成60角,AC=8,BD=8,M、N分别为AB、CD的中点,则线段MN的长是 .
【答案】
分析:取BC中点P,连接PN,MP,可得NP=4,MP=4,∠MPN(或其补角)为AC与BD成的角,再利用余弦定理,可求MN.
解答:解:取BC中点P,连接PN,MP
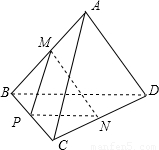
因为M,N分别为AB和CD的中点,所以PN和MP分别是△BCD和△ABC的中位线
所以NP平行且等于

BD,MP平行且等于

AC,
所以NP=4,MP=4,∠MPN(或其补角)为AC与BD成的角,
∵AC与BD成60°角,
∴∠MPN=60°或120°
根据余弦定理:MN
2=MP
2+NP
2-2MP×NP×cos∠MPN
所以MN
2=16+16-2×4×4×0.5=16或MN
2=16+16+2×4×4×0.5=48
所以MN=4或
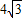
故答案为4或
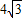
.
点评:本题考查异面直线所成的角,考查余弦定理的运用,考查学生的计算能力,正确作出异面直线所成的角是关键.


 BD,MP平行且等于
BD,MP平行且等于 AC,
AC,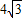
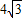 .
.

 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.