
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
【答案】(1) (RP)∩Q={x|-2≤x<4}.(2) (-∞,2].
【解析】试题分析:(1)先求集合Q以及RP,再求(RP)∩Q;(2)由P∪Q=Q,得PQ.再根据P为空集与非空分类讨论,结合数轴求实数a的取值范围.
试题解析:解:(1)因为a=3,所以集合P={x|4≤x≤7}.
所以RP={x|x<4或x>7},
Q={x|1≤2x+5≤15}={x|-2≤x≤5},
所以(RP)∩Q={x|-2≤x<4}.
(2)因为P∪Q=Q,所以PQ.
①当a+1>2a+1,即a<0时,P=,
所以PQ;
②当a≥0时,因为PQ,
所以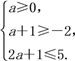 所以0≤a≤2.
所以0≤a≤2.
综上所述,实数a的取值范围为(-∞,2].


科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为![]() ,则由此可估计
,则由此可估计![]() 的近似值为( )
的近似值为( )
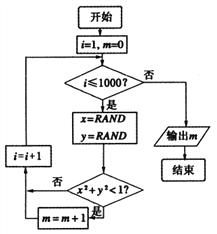
A. 3.119 B. 3.124 C. 3.132 D. 3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,圆
,圆![]() ,点
,点![]() 为抛物线
为抛物线![]() 上的动点,
上的动点,![]() 为坐标原点,线段
为坐标原点,线段![]() 的中点
的中点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 上的点,过点
上的点,过点![]() 作圆
作圆![]() 的两条切线,分别与
的两条切线,分别与![]() 轴交于
轴交于![]() 两点.
两点.
求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生1 000名,经调查,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学,如果以身高达165 cm作为达标的标准,对抽取的100名学生,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
(1)完成上表;
(2)能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com