
函数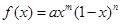 在区间
在区间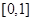 上的图像如图所示,则
上的图像如图所示,则 、
、 的值可能是( )
的值可能是( )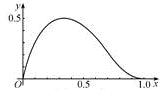
A.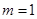 , , |
B.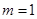 , ,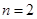 |
C. , , |
D. , , |
B
解析试题分析:原函数的极大值点小于0.5.把答案代入验证看哪个对应的极值点符合要求即可得出答案.解:由于本题是选择题,可以用代入法来作,由图得,原函数的极大值点小于0.5.当m=1,n=1时,f(x)=ax(1-x)=-a(x-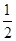 )2+
)2+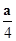 .在x=
.在x=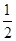 处有最值,故A错;当m=1,n=2时,f(x)=axm(1-x)n=ax(1-x)2=a(x3-2x2+x),所以f'(x)=a(3x-1)(x-1),令f'(x)=0⇒x=
处有最值,故A错;当m=1,n=2时,f(x)=axm(1-x)n=ax(1-x)2=a(x3-2x2+x),所以f'(x)=a(3x-1)(x-1),令f'(x)=0⇒x=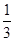 ,x=1,即函数在x=
,x=1,即函数在x=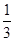 处有最值,故B对;当m=2,n=1时,f(x)=axm(1-x)n=ax2(1-x)=a(x2-x3),有f'(x)=a(2x-3x2)=ax(2-3x),令f'(x)=0⇒x=0,x=
处有最值,故B对;当m=2,n=1时,f(x)=axm(1-x)n=ax2(1-x)=a(x2-x3),有f'(x)=a(2x-3x2)=ax(2-3x),令f'(x)=0⇒x=0,x=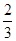 ,即函数在x=
,即函数在x=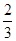 处有最值,故C错;当m=3,n=1时,f(x)=axm(1-x)n=ax3(1-x)=a(x3-x4),有f'(x)=ax2(3-4x),令f'(x)=0,⇒x=0,x=
处有最值,故C错;当m=3,n=1时,f(x)=axm(1-x)n=ax3(1-x)=a(x3-x4),有f'(x)=ax2(3-4x),令f'(x)=0,⇒x=0,x=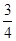 ,即函数在x=
,即函数在x=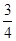 处有最值,故D错.故选 B
处有最值,故D错.故选 B
考点:函数的最值(极值)点与导函数之间的关系
点评:本题主要考查函数的最值(极值)点与导函数之间的关系.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.本本题考查利用极值求对应变量的值.可导函数的极值点一定是导数为0的点,但导数为0的点不一定是极值点


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com