
【题目】如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E. 
(1)求证:ABDE=BCCE;
(2)若AB=8,BC=4,求线段AE的长.
【答案】
(1)证明:连接BE,OC,AC,OC∩BE=F,则
∵CD是圆O的切线,
∴OC⊥l,
∵AD⊥l,∴AD∥OC,
∵AB是圆O的直径,∴AD⊥BE,
∵AD⊥l,∴l∥BE,
∴∠DCE=∠CBE=∠CAB,
∵∠EDC=∠BCA=90°,
∴△EDC∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ABDE=BCCE

(2)解:由(1)可知四边形EFCD是矩形,
∴DE=CF,
∵圆O的直径AB=8,BC=4,
∴∠ABC=60°
∴△OBC是等边三角形,
∴∠EBA=30°,AE=4
【解析】(1)连接BE,OC,OC∩BE=F,证明△EDC∽△BCA,即可证明ABDE=BCCE;(2)证明四边形EFCD是矩形,△OBC是等边三角形,即可得出结论.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1+a|x|),a∈R.
(1)当a=-1时,求函数![]() 的零点;
的零点;
(2)若函数f(x)在R上递增,求实数a的取值范围;
(3)设关于x的不等式f(x+a)<f(x)的解集为A,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
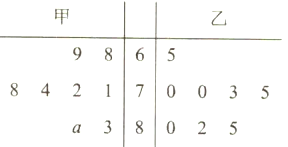
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-P2-x,则下列结论正确的是( )
A. ![]() ,
,![]() 为奇函数且为R上的减函数
为奇函数且为R上的减函数
B. ![]() ,
,![]() 为偶函数且为R上的减函数
为偶函数且为R上的减函数
C. ![]() ,
,![]() 为奇函数且为R上的增函数
为奇函数且为R上的增函数
D. ![]() ,
,![]() 为偶函数且为R上的增函数
为偶函数且为R上的增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.若sin(A﹣B)+sinC= ![]() sinA.
sinA.
(1)求角B的值;
(2)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①命题“若x≥2且y≥3,则x+y≥5”为假命题.
②命题“若x2-4x+3=0,则x=3”的逆否命题为:“若x≠3,则x2-4x+3≠0”.
③“x>1”是“|x|>0”的充分不必要条件
④关于x的不等式|x+1|+|x-3|≥m的解集为R,则m≤4.
其中所有正确命题的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com