Question

【题目】已知f（x）为定义在R上的偶函数，当x≤﹣1时，f（x）=x+b，且f（x）的图象经过点（﹣2，0），在y=f（x）的图象中有一部分是顶点为（0，2），过点（﹣1，1）的一段抛物线．
（1）试求出f（x）的表达式；
（2）求出f（x）的值域．

Answer 1

【答案】
（1）解：当x≤﹣1时，f（x）=x+b，且f（x）的图象经过点（﹣2，0），

则b﹣2=0，解得：b=2，即f（x）=x+2；

由于f（x）为定义在R上的偶函数，当x≥1时，f（x）=f（﹣x）=﹣x+2；

y=f（x）的图象中有一部分是顶点为（0，2），过点（﹣1，1）的一段抛物线．

设y=ax2+2，过点（﹣1，1），则a+2=﹣1，解得：y=﹣x2+2，

可见当﹣1＜x＜1时，f（x）=﹣x2+2；

则f（x）=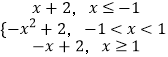

（2）解：当x≤﹣1时，f（x）=x+2≤1；

当﹣1＜x＜1时，f（x）=﹣x2+2∈（1，2]；

当x≥1时，f（x）=﹣x+2≤1；

函数的值域为（﹣∞，2]

【解析】(1)由待定系数法可求出当x≤﹣1时函数的解析式，再根据函数的奇偶性得出当x≥1时，f（x）=f（﹣x）=﹣x+2，由题意可知根据二次函数图像的性质可求出﹣1＜x＜1时的函数解析式，进而得到在不同的区间上的f（x）的解析式。
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识，掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．