
【题目】选修4-4:坐标系与参数方程
已知在极坐标系中,点![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,以极点为原点,极轴为
的中点,以极点为原点,极轴为![]() 轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线
轴的正半轴,并在两坐标系中取相同的长度单位,建立平面直角坐标系,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:⑴对于定义域上的任意
同时满足:⑴对于定义域上的任意![]() ,恒有
,恒有![]() ; ⑵对于定义域上的任意
; ⑵对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中: ①
为“理想函数”.给出下列四个函数中: ①![]() ,②
,②![]() , ③
, ③![]() ,④
,④ ,能被称为“理想函数”的有_____________(填相应的序号).
,能被称为“理想函数”的有_____________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,底面
,底面![]() 是梯形,AB∥CD,
是梯形,AB∥CD,![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,![]() ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且![]() .
.
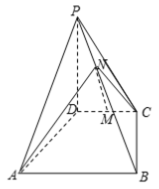
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为![]() ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:

(1)求频率分布直方图中![]() 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数
的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数![]() 和中位数
和中位数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加某数学竞赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下.
理科:79,81,81,79,94,92,85,89
文科:94,80,90,81,73,84,90,80
画出理科、文科两组同学成绩的茎叶图;

(2)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥比较好;
(3)若在成绩不低于90分的同学中随机抽出3人进行培训,求抽出的3人中既有理科组同学又有文科组同学的概率.
(参考公式:样本数据x1,x2,…,xn的方差:
s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2+…+(xn-
)2+…+(xn-![]() )2],其中
)2],其中![]() 为样本平均数)
为样本平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且两焦点与短轴的一个顶点的连线构成等腰直角三角形.
,且两焦点与短轴的一个顶点的连线构成等腰直角三角形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,试问:是否存在一个定点
两点,试问:是否存在一个定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.

(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com