
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() 和直线
和直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,并且被圆
,并且被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的方程.
的方程.
【答案】(1)(x-1)2+(y+2)2=2.(2)x=2或3x-4y-6=0.
【解析】
(1)根据圆的弦的中垂线过圆心以及圆心到切线的距离等于半径可求得圆心坐标及半径的大小,从而可得结果;(2)若直线斜率不存在,符合题意;若直线斜率存在,可设直线方程为![]() ,利用点到直线距离公式列方程可求出
,利用点到直线距离公式列方程可求出![]() 的值,从而可得结果.
的值,从而可得结果.
(1)由题知,线段AB的中点M(1,-2), ![]() ,
,
线段AB的垂直平分线方程为![]() ,即
,即![]() ,
,
设圆心的坐标为C(a,-a-1),
则![]() ,
,
化简,得a2-2a+1=0,解得a=1.∴C(1,-2),
半径r=|AC|=![]() =
=![]() .
.
∴圆C的方程为(x-1)2+(y+2)2=2.
(2)由题知圆心C到直线l的距离![]() ,
,
①当直线l的斜率不存在时,直线l的方程为x=2,此时直线l被圆C截得的弦长为2,
满足条件.
②当直线l的斜率存在时,设直线l的方程为![]() ,由题意得
,由题意得![]() ,
,
解得k=![]() ,
,
∴直线l的方程为y=![]() (x-2).
(x-2).
综上所述,直线l的方程为x=2或3x-4y-6=0.


科目:高中数学 来源: 题型:
【题目】某公司生产一批A产品需要原材料500吨,每吨原材料可创造利润12万元.该公司通过设备升级,生产这批A产品所需原材料减少了x吨,且每吨原材料创造的利润提高0.5x%;若将少用的x吨原材料全部用于生产公司新开发的B产品,每吨原材料创造的利润为12(a﹣ ![]() x)万元(a>0).
x)万元(a>0).
(1)若设备升级后生产这批A产品的利润不低于原来生产该批A产品的利润,求x的取值范围.
(2)若生产这批B产品的利润始终不高于设备升级后生产这批A产品的利润,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值.
的单调区间和极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据导数几何意义得![]() ,再与
,再与![]() 联立方程组解得
联立方程组解得![]() ,
, ![]() (2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1)![]() ,切线为
,切线为![]() ,即斜率
,即斜率![]() ,纵坐标
,纵坐标![]()
即![]() ,
, ![]() ,解得
,解得![]() ,
, ![]()
解析式![]()
(2)![]()
![]()
![]() ,定义域为
,定义域为![]()
得到![]() 在
在![]() 单增,在
单增,在![]() 单减,在
单减,在![]() 单增
单增
极大值![]() ,极小值
,极小值![]() .
.
【题型】解答题
【结束】
20
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
, ![]() 底面
底面![]() ,
,
![]() ,
, ![]() ,
, ![]() 是
是![]() 上点,且
上点,且![]() 平面
平面![]() .
.
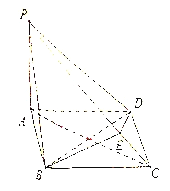
(1)求证: ![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若关于
:若关于![]() 的方程
的方程![]() 无实数根,则
无实数根,则![]() ;命题
;命题![]() :若关于
:若关于![]() 的方程
的方程![]() 有两个不相等的正实数根,则
有两个不相等的正实数根,则![]() .
.
(1)写出命题![]() 的否命题,并判断命题
的否命题,并判断命题![]() 的真假;
的真假;
(2)判断命题“![]() 且
且![]() ”的真假,并说明理由.
”的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,且点
,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于异于
相交于异于![]() 的不同两点
的不同两点![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣1:几何证明选讲)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ![]() ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示.
得到的频率分布直方图如图所示.

(1)分别求第![]() ,
, ![]() ,
, ![]() 组的频率;
组的频率;
(2)若该校决定在笔试成绩高的第![]() ,
, ![]() ,
, ![]() 组中用分层抽样抽取
组中用分层抽样抽取![]() 名学生进入第二轮面试,求第
名学生进入第二轮面试,求第![]() ,
, ![]() ,
, ![]() 组每组各抽取多少名学生进入第二轮面试?
组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受甲考官的面试,求第
名学生接受甲考官的面试,求第![]() 组至少有一名学生被甲考官面试的概率.
组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 为平面上一动点,
为平面上一动点,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)不过原点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交点的纵坐标为1,求
交点的纵坐标为1,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:


(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率.
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
K2=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com