练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，空间四边形ABCD中，AB=CD，AB⊥CD，E、F分别为BC、AD的中点，则EF和AB所成的角为

    【答案】45°
    【解析】解：取AC的中点M，连接EM、FM．
    ∵E为BC的中点，∴EM∥AB且EM=AB；
    同理：FM∥CD且FM=CD，
    ∴∠FEM为异面直线AB、EF所成的角，
    又∵AB⊥CD，AB=CD，∴FM=EM，FM⊥EM，
    ∴△EFM为等腰直角三角形，∴∠FEM=45°
    故答案是45°．

    【考点精析】关于本题考查的异面直线及其所成的角，需要了解异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，M、N、K分别是正方体ABCD﹣A1B1C1D1的棱AB，CD，C1D1的中点．求证：
    （1）AN∥平面A1MK；
    （2）MK⊥平面A1B1C．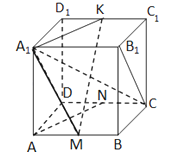

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2 ， AD=2，求四边形绕AD旋转一周所围成几何体的表面积及体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=ln（x2﹣x）的定义域为（　　）
    A.（0，1）
    B.[0，1]
    C.（﹣∞，0）∪（1，+∞）
    D.（﹣∞，0]∪[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某组合体的三视图，则内部几何体的体积的最大值为（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在底面为平行四边形的四棱锥P﹣ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．
    （Ⅰ）求证：AC⊥PB；
    （Ⅱ）求证：PB∥平面AEC．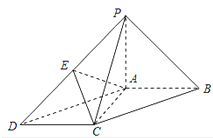

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，过椭圆： （）焦点的直线交于两点， 为的中点，且的斜率为9.

    （Ⅰ）求的方程；

    （Ⅱ）是的左、右顶点， 是上的两点，若，求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知梯形ABCD中，AD∥BC，∠ABC=∠BAD=π/2，AB=BC=2AD=4，E，F分别是AB，CD上的点，EF∥BC，AE=x，G是BC的中点，沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF．
    （1）当x=2时，①求证：BD⊥EG；②求二面角D﹣BF﹣C的余弦值；
    （2）三棱锥D﹣FBC的体积是否可能等于几何体ABE﹣FDC体积的一半？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】非空集合A中的元素个数用（A）表示，定义（A﹣B）= ，若A={﹣1，0}，B={x||x2﹣2x﹣3|=a}，且（A﹣B）≤1，则a的所有可能值为（ ）
    A.{a|a≥4}
    B.{a|a＞4或a=0}
    C.{a|0≤a≤4}
    D.{a|a≥4或a=0}

    查看答案和解析>>

    同步练习册答案