
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 上一点,
上一点, ![]() ,试确定
,试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)在梯形ABCD中,过点作B作BH⊥CD于H,通过面面垂直的判定定理即得结论;(2)过点Q作QM∥BC交PB于点M,过点M作MN⊥BD于点N,连QN.则∠QNM是二面角Q-BD-P的平面角,在Rt三角形MNQ中利用tan∠MNQ=QM/MN计算即可
试题解析:(1)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]()
在梯形![]() 中,过点
中,过点![]() 作
作![]() 于
于![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
又在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ……………2分
……………2分
∵![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,……………4分
,……………4分
∴![]() 平面
平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .∵
.∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .……………6分
.……………6分
(1)过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 于点
于点![]() ,连
,连![]() .
.
由(2)可知![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]()
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,∴
的平面角,∴![]() ……………8分
……………8分
∵![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由(1)知![]() ,∴
,∴![]() ,又∵
,又∵![]()
∵![]() ∥
∥![]() ,∴
,∴![]() ,∴
,∴![]() ……10分
……10分
∵![]() ,∴
,∴![]() ,
,
∴![]() .……………12分
.……………12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,由三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
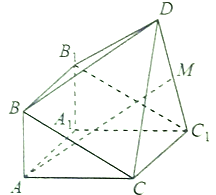
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 是偶函数,
是偶函数,![]() 为实常数.
为实常数.
(1)求![]() 的值;
的值;
(2)当![]() 时,是否存在
时,是否存在![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的函数值组成的集合也是
上的函数值组成的集合也是![]() ,若存在,求出
,若存在,求出![]() ,
,![]() 的值;否则,说明理由.
的值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com