
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的左顶点和上顶点,若
的左顶点和上顶点,若![]() 的中点的纵坐标为
的中点的纵坐标为![]() .
.![]() 分别为
分别为![]() 的左、右焦点.
的左、右焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,
,![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以
在以![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年 份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
![]() =
= ,
,![]() =
=![]() -
-![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,![]() ,
,![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,M是BC的中点,N在线段DC上,
,M是BC的中点,N在线段DC上,![]() ,求证:
,求证:![]() 平面AMN;
平面AMN;
(2)当BP与平面ACD所成角最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足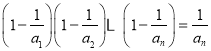 ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,若对于一切
,若对于一切![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 中存在某项
中存在某项![]() 满足
满足![]() 成等差数列?若存在,求出符合题意的
成等差数列?若存在,求出符合题意的![]() 的集合;若不存在,请说明理由.
的集合;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com