
【题目】已知 ![]() 是双曲线
是双曲线 ![]() 的右焦点,过点
的右焦点,过点 ![]() 作
作 ![]() 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ![]() ,线段
,线段 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,记点
,记点 ![]() 到
到 ![]() 的两条渐近线的距离之积为
的两条渐近线的距离之积为 ![]() ,若
,若 ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.![]()
B.2
C. 3
D.4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=2sin(2x+ ![]() ),将f(x)图象上每个点的横坐标缩短为原来的一半之后成为函数y=g(x),则g(x)的图象的一条对称轴方程为( )
),将f(x)图象上每个点的横坐标缩短为原来的一半之后成为函数y=g(x),则g(x)的图象的一条对称轴方程为( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的菱形,且∠BAD= ![]() ,AA1⊥平面ABCD,AA1=1,设E为CD中点
,AA1⊥平面ABCD,AA1=1,设E为CD中点 
(1)求证:D1E⊥平面BEC1
(2)点F在线段A1B1上,且AF∥平面BEC1 , 求平面ADF和平面BEC1所成锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
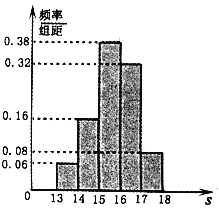
(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①第二象限角比第一象限角大;②设![]() 是第二象限角,则
是第二象限角,则![]() ;③三角形的内角是第一象限角或第二象限角;④函数
;③三角形的内角是第一象限角或第二象限角;④函数![]() 是最小正周期为
是最小正周期为![]() 的周期函数;⑤在△ABC中,若
的周期函数;⑤在△ABC中,若![]() ,则A>B.其中正确的是___________ (写出所有正确说法的序号)
,则A>B.其中正确的是___________ (写出所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用另一种形式表示下列集合:
(1){绝对值不大于3的整数};
(2){所有被3整除的数};
(3){x|x=|x|,x∈Z且x<5};
(4){x|(3x-5)(x+2)(x2+3)=0,x∈Z}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)设f(x)、g(x)、h(x)是定义域为R的三个函数,对于命题:①若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是增函数,则f(x)、g(x)、h(x)均是增函数;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T为周期的函数,则f(x)、g(x)、h(x)均是以T为周期的函数,下列判断正确的是( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com