
【题目】已知棱长为1的正方体![]() ,点
,点![]() 是四边形
是四边形![]() 内(含边界)任意一点,
内(含边界)任意一点,![]() 是
是![]() 中点,有下列四个结论:
中点,有下列四个结论:
①![]() ;②当
;②当![]() 点为
点为![]() 中点时,二面角
中点时,二面角![]() 的余弦值
的余弦值![]() ;③
;③![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;④当
;④当![]() 时,点
时,点![]() 的轨迹长为
的轨迹长为![]() .
.
其中所有正确的结论序号是( )
A.①②③B.①③④C.②③④D.①②④
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,N为CD的中点,M是AC上一点.
中,N为CD的中点,M是AC上一点.
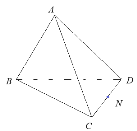
(1)若M为AC的中点,求证:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直线AC与平面BMN所成的角的余弦值。
,求直线AC与平面BMN所成的角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 、
、![]() ;
;
(2)设曲线![]() 与
与![]() 轴负半轴的交点为点
轴负半轴的交点为点![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的实数
,求证:对于任意的实数![]() ,都有
,都有![]() ;
;
(3)若关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B是抛物线![]() 上关于轴对称的两点,点E是抛物线C的准线与x轴的交点.
上关于轴对称的两点,点E是抛物线C的准线与x轴的交点.
(1)若![]() 是面积为4的直角三角形,求抛物线C的方程;
是面积为4的直角三角形,求抛物线C的方程;
(2)若直线BE与抛物线C交于另一点D,证明:直线AD过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】完成下列抽样调查,较为合理的抽样方法依次是( )
①从![]() 件产品中抽取
件产品中抽取![]() 件进行检查;
件进行检查;
②某校高中三个年级共有![]() 人,其中高一
人,其中高一![]() 人、高二
人、高二![]() 人、高三
人、高三![]() 人,为了了解学生对数学的建议,拟抽取一个容量为
人,为了了解学生对数学的建议,拟抽取一个容量为![]() 的样本;
的样本;
③某剧场有![]() 排,每排有
排,每排有![]() 个座位,在一次报告中恰好坐满了听众,报告结束后,为了了解听众意见,需要请
个座位,在一次报告中恰好坐满了听众,报告结束后,为了了解听众意见,需要请![]() 名听众进行座谈.
名听众进行座谈.
A.简单随机抽样,系统抽样,分层抽样;B.分层抽样,系统抽样,简单随机抽样;
C.系统抽样,简单随机抽样,分层抽样;D.简单随机抽样,分层抽样,系统抽样;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com