
分析 (1)根据已知等式确定出a2,a3,得出{an}的通项公式即可;
(2)表示出{$\frac{1}{a_n}$}的前n项和Tn,根据前n项和Tn为递增数列,确定出Tn的范围,即可得证.
解答 解:(1)由S2=$\frac{4}{3}$a2,a1=1,得到3(a1+a2)=4a2,
解得:a2=3a1=3;
由S3=$\frac{5}{3}$a3得3(a1+a2+a3)=5a3,
解得:a3=$\frac{3}{2}$(a1+a2)=6.
由题设知a1=1,
当n>1时有an=Sn-Sn-1=$\frac{n+2}{3}$an-$\frac{n+1}{3}$an-1,
整理得:an=$\frac{n+1}{n-1}$an-1.
于是a1=1,a2=$\frac{3}{1}$a1,a3=$\frac{4}{2}$a2,…,an-1=$\frac{n}{n-2}$an-2,an=$\frac{n+1}{n-1}$an-1,
将以上n个等式两端分别相乘,整理得an=$\frac{n(n+1)}{2}$,
综上,{an}的通项公式an=$\frac{n(n+1)}{2}$;
(2)∵$\frac{1}{{a}_{n}}$=$\frac{2}{n(n+1)}$,
∴Tn=2[$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{n(n+1)}$]=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)=2-$\frac{2}{n+1}$<2,即Tn<2,
又Tn+1>Tn,{Tn}单调增,
∴Tn>=T1=1,
则1≤Tn<2.
点评 此题考查了数列的求和,确定数列的通项公式,拆项法,以及数列的递推式,熟练掌握数列的性质是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
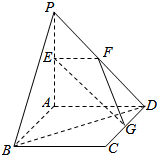 平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点
平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
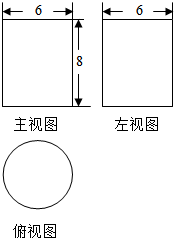 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{3}$] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$] | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com