Question

设n＝2³¹?3¹⁹．n²有多少个小于n，但不能整除n的正整数因子？

Answer 1

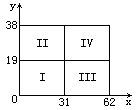
解析：n²的因子必为2^α?3^β形，其中0≤α≤62，0≤β≤38．

于是(α，β)是属于图中矩形的格点，显然对I、IV中的格点(α，β)，2^α．3^β不满足要求(2^α?3^β|n或2^α?3^β≥n)，II中任一格点(约定β＝19或α＝31的点属于I或IV，不属于II或III)(α，β)，若2^α?3^β≥n，则对III中格点(62－α，31－β)，有2^62－α?3^31－β＜n．反之，对III中格点(α，β)，若2^α?3^β≥n，则对II中格点(62－α，31－β)，有2^62－α?3^31－β＜n．因此II、III中恰有一半的格点(α，β)，使2^α?3^β满足要求．即所求的正整数因子个数为

19×31＝589