
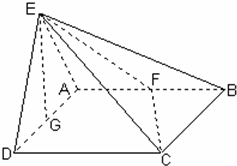
 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角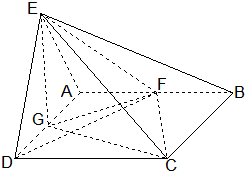 解:(1)证明:如图所示,∵△ADE是等边三角形,
解:(1)证明:如图所示,∵△ADE是等边三角形, ,
,
 ,GF=
,GF= ,FC=
,FC=

 ,S△EFC=3a2
,S△EFC=3a2
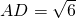


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
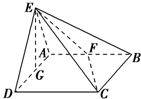 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角查看答案和解析>>
科目:高中数学 来源: 题型:
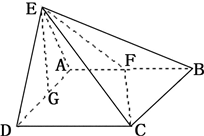
| 6 |
查看答案和解析>>
科目:高中数学 来源:河南省模拟题 题型:解答题
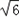 ,求三棱锥F﹣EGC的体积.
,求三棱锥F﹣EGC的体积. 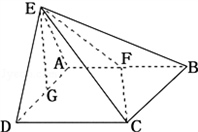
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市巴县中学高二(下)期末复习优生训练4(文科)(解析版) 题型:解答题
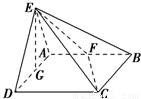 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com