
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为4,椭圆
的距离为4,椭圆![]()
![]() 的离心率
的离心率![]() ,且过抛物线的焦点
,且过抛物线的焦点![]() .
.
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两不同点,交
两不同点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)抛物线的方程为![]() ,椭圆的标准方程为
,椭圆的标准方程为![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)利用抛物线C1:y2=2px上一点M(3,y0)到其焦点F的距离为4;求出p,即可得到抛物线方程,通过椭圆的离心率e=![]() ,,且过抛物线的焦点F(1,0)求出a,b,即可得到椭圆的方程;
,,且过抛物线的焦点F(1,0)求出a,b,即可得到椭圆的方程;
(2)直线l1的斜率必存在,设为k,设直线l与椭圆C2交于A(x1,y1),B(x2,y2),求出直线l的方程为y=k(x-1),N(0,-k),联立直线与椭圆的方程,利用韦达定理以及判别式,通过向量关系式即可求出λ+μ为定值.
试题解析:
(Ⅰ)抛物线的准线为![]() , 所以
, 所以![]() ,所以
,所以![]()
抛物线的方程为![]()
所以![]() ,
,![]() ,解得
,解得![]() 所以椭圆的标准方程为
所以椭圆的标准方程为![]()
(Ⅱ)直线![]() 的斜率必存在,设为
的斜率必存在,设为![]() ,设直线
,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]()
则直线![]() 的方程为
的方程为![]() ,
,![]()
联立方程组:![]()
所以![]()
![]() ,
,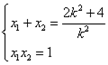 (*)
(*)
由![]() 得:
得:
![]() 得:
得:![]()
所以![]()
将(*)代入上式,得![]()


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , a4+a7=20,对任意的k∈N都有Sk+1=3Sk+k2 .
(I) 求数列{an}的通项公式;
(Ⅱ)数列{bn}定义如下:2mbm(m∈N*)是使不等式an≥m成立所有n中的最小值,求{bn}的通项公式及{(﹣1)m﹣1bm}的前2m项和T2m .
查看答案和解析>>
科目:高中数学 来源: 题型:
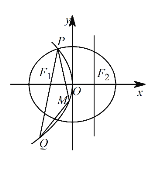
【题目】如图,设抛物线 ![]() :
:![]() 的准线
的准线 ![]() 与
与 ![]() 轴交于椭圆
轴交于椭圆 ![]() :
:![]() 的右焦点
的右焦点 ![]() ,
,![]() 为
为 ![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为 ![]() ,抛物线
,抛物线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 轴上方一点
轴上方一点 ![]() ,连接
,连接 ![]() 并延长交
并延长交 ![]() 于点
于点 ![]() ,
,![]() 为
为 ![]() 上一动点,且在
上一动点,且在 ![]() ,
,![]() 之间移动.
之间移动.
(1)当![]() 时,求
时,求 ![]() 的方程;
的方程;
(2)若 ![]() 的边长恰好是三个连续的自然数。求
的边长恰好是三个连续的自然数。求![]() 到直线
到直线![]() 距离的最大值以及此时
距离的最大值以及此时![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:条件p:实数t满足使对数log2(﹣2t2+7t﹣5)有意义;条件q:实数t满足不等式t2﹣(a+3)t+a+2<0
(1)若命题¬p为真,求实数t的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
(Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2 ![]() (ω>0)的最小正周期为3π.
(ω>0)的最小正周期为3π.
(I)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c, ![]() a=2csinA,并且f(
a=2csinA,并且f( ![]() A+
A+ ![]() )=
)= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过
,过![]() 作与
作与![]() 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 的斜率存在且不为0,直线
的斜率存在且不为0,直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 中点为
中点为![]() ,
,![]() 为原点,直线
为原点,直线![]() 交
交![]() 于点
于点![]() ,若以
,若以![]() 为直径的圆过右焦点
为直径的圆过右焦点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com