
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
分析 如图所示,EO⊥平面ABCD,OF⊥AB,EF⊥AB,则∠EBO为BE与平面ABCD所成角,设EB=2a,求出EO=$\sqrt{2}$a,即可求出BE与平面ABCD所成角.
解答  解:如图所示,EO⊥平面ABCD,OF⊥AB,EF⊥AB,
解:如图所示,EO⊥平面ABCD,OF⊥AB,EF⊥AB,
则∠EBO为BE与平面ABCD所成角,
设EB=2a,则EF=$\sqrt{3}$a,OF=a,
∴EO=$\sqrt{2}$a,
∴sin∠EBO=$\frac{\sqrt{2}}{2}$,
∵0<∠EBO<$\frac{π}{2}$,
∴∠EBO=$\frac{π}{4}$.
故选C.
点评 本题考查线面角,考查学生的计算能力,正确作出线面角是关键.


科目:高中数学 来源: 题型:解答题
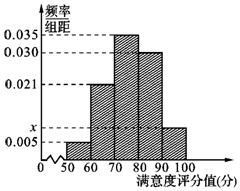 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )| A. | 求24名男生的达标率 | B. | 求24名男生的不达标率 | ||
| C. | 求24名男生的达标人数 | D. | 求24名男生的不达标人数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
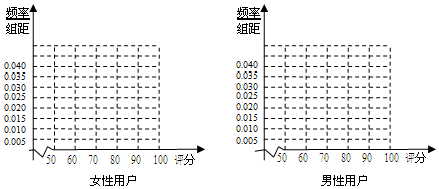
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com