
(本小题14分)
在等差数列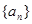 中,
中,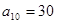 ,
, .
.
(1)求数列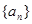 的通项
的通项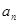 ;
;
(2)令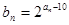 ,证明:数列
,证明:数列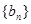 为等比数列;
为等比数列;
(3)求数列 的前
的前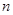 项和
项和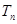 .
.
(1) ;
;
(2)见解析
(3) 

解析试题分析:(1)先由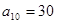 ,
, ,可建立关于a1和d的方程求出a1和d的值,从而求出通项
,可建立关于a1和d的方程求出a1和d的值,从而求出通项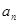 .
.
(2)再(1)的基础上可求出 ,再利用等比数列的定义可判断出
,再利用等比数列的定义可判断出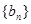 为等比数列;
为等比数列;
(3)由于 的通项为
的通项为 显然要采用错位相减的方法求和。
显然要采用错位相减的方法求和。
(1)设数列 首项为
首项为 ,公差为
,公差为
依题意得 ,………2分
,………2分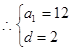 ………………3分
………………3分 ……………4分
……………4分
(2)
 是以
是以 =4为首项,4为公比的等比数列。………………………8分
=4为首项,4为公比的等比数列。………………………8分
(3) ……………………9分
……………………9分 …………………11分
…………………11分
考点:等差数列的通项公式,等比数列的定义及通项公式及其前n项和公式,错位相减法求和。
点评:等差数列及等比数列的定义是判断数列是否是等差或等比数列的依据,并且要注意结合通项公式的特点判断选用何种方法求和,本题是一个等差数列与一个等比数列的积所以应采用错位相减法求和.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
等差数列{an}不是常数列,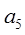 =10,且
=10,且 是等比数列{
是等比数列{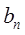 }的第1,3,5项,且
}的第1,3,5项,且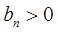 .
.
(1)求数列{ }的第20项,(2)求数列{
}的第20项,(2)求数列{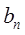 }的通项公式.
}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知等比数列{an}的各项均为正数,且 2a1 +3a2 =1, =9a2a6.
=9a2a6.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)设 bn=log3a1 +log3a2 +…+ log3an,求 的前n项和Tn;
的前n项和Tn;
(Ⅲ)在(Ⅱ)的条件下,求使  ≥ (7? 2n)Tn恒成立的实数k 的取值范围.
≥ (7? 2n)Tn恒成立的实数k 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,
, (
( ).
).
(Ⅰ)证明数列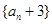 是等比数列,求出数列
是等比数列,求出数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和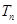 ;
;
(Ⅲ)数列 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com