
A、
| ||
B、
| ||
C、
| ||
D、
|
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:扬州大学附属中学高一上学期期末测试卷高一数学[上学期] 题型:044
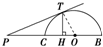
已知点T是半圆O的直径AB上一点,AB=2、OT=t(0<t<1),以AB为直腰作直角梯形![]() ,使
,使![]() 垂直且等于AT,使
垂直且等于AT,使![]() 垂直且等于BT,
垂直且等于BT,![]() 交半圆于P、Q两点,建立如图所示的直角坐标系.
交半圆于P、Q两点,建立如图所示的直角坐标系.
(Ⅰ)写出直线![]() 的方程;
的方程;
(Ⅱ)计算出点P、Q的坐标;
(Ⅲ)证明:沿PT射出的光线,经AB反射后,反射光线通过点Q.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com