
分析 (1)推导出$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{2n}$,由此利用累乘法能求出an=$\frac{n}{{2}^{n-1}}$,从而求出$\frac{{a}_{n}}{n}$=($\frac{1}{2}$)n-1,由此能证明数列{$\frac{{a}_{n}}{n}$}为首项是1,公比为$\frac{1}{2}$的等比数列.
(2)由an=$\frac{n}{{2}^{n-1}}$=$n•(\frac{1}{2})^{n-1}$,利用错位相减法能求出{an}数列的前n项和.
解答 证明:(1)∵在数列{an}中,a1=1,an+1=$\frac{n+1}{2n}{a_n}$,n∈N*,
∴$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n+1}{2n}$,
∴an=${a}_{1}×\frac{{a}_{2}}{{a}_{1}}×\frac{{a}_{3}}{{a}_{2}}×\frac{{a}_{4}}{{a}_{3}}×…×\frac{{a}_{n}}{{a}_{n-1}}$
=1×$\frac{2}{2}×\frac{3}{4}×\frac{4}{6}×…×\frac{n}{2(n-1)}$=$\frac{n}{{2}^{n-1}}$.
∴$\frac{{a}_{n}}{n}$=$\frac{1}{{2}^{n-1}}$=($\frac{1}{2}$)n-1,
∴数列{$\frac{{a}_{n}}{n}$}为首项是1,公比为$\frac{1}{2}$的等比数列.
(2)∵an=$\frac{n}{{2}^{n-1}}$=$n•(\frac{1}{2})^{n-1}$,∴{an}数列的前n项和:
Tn=1×$(\frac{1}{2})^{0}$+2×$\frac{1}{2}+3×(\frac{1}{2})^{2}+4×(\frac{1}{2})^{3}+…+n×(\frac{1}{2})^{n-1}$,①
$\frac{1}{2}$Tn=1×$\frac{1}{2}$+$2×(\frac{1}{2})^{2}+3×(\frac{1}{2})^{3}+4×(\frac{1}{2})^{4}$+…+n×($\frac{1}{2}$)n,②
①-②,得:
$\frac{1}{2}{T}_{n}$=1+$\frac{1}{2}+(\frac{1}{2})^{2}+(\frac{1}{2})^{3}+…+(\frac{1}{2})^{n-1}$-n×($\frac{1}{2}$)n
=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$-n×($\frac{1}{2}$)n
=2-(n+2)×($\frac{1}{2}$)n,
∴Tn=4-(n+2)×($\frac{1}{2}$)n-1.
点评 本题考查等比数列的证明,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意累乘法和错位相减法的合理运用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
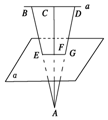 如图a∥α,A是α的另一侧的点,B,C,D∈a,线段AB,AC,AD交α于E,F,G,若BD=4,AB=9,AE=5,则EG=( )
如图a∥α,A是α的另一侧的点,B,C,D∈a,线段AB,AC,AD交α于E,F,G,若BD=4,AB=9,AE=5,则EG=( )| A. | 5 | B. | $\frac{15}{9}$ | C. | 3 | D. | $\frac{20}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22-n | B. | 2n-2 | C. | 2n+2 | D. | 2-n-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com