
给出命题:若 是正常数,且
是正常数,且 ,
, ,则
,则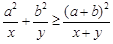 (当且仅当
(当且仅当 时等号成立). 根据上面命题,可以得到函数
时等号成立). 根据上面命题,可以得到函数 (
( )的最小值及取最小值时的x值分别为( )
)的最小值及取最小值时的x值分别为( )
A.11+6 ,
, B.11+6
B.11+6 ,
, C.5,
C.5, D.25,
D.25,
科目:高中数学 来源: 题型:
| Tn |
| Tm |
| Tn |
| Tm |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏苏州高级中学高三12月月考数学试卷(解析版) 题型:解答题
设 是各项均为非零实数的数列
是各项均为非零实数的数列 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上:
命题 :
: 是等差数列;命题
是等差数列;命题 :等式
:等式 对任意
对任意 (
( )恒成立,其中
)恒成立,其中 是常数。
是常数。
⑴若 是
是 的充分条件,求
的充分条件,求 的值;
的值;
⑵对于⑴中的 与
与 ,问
,问 是否为
是否为 的必要条件,请说明理由;
的必要条件,请说明理由;
⑶若 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
( )和正数M,数列
)和正数M,数列 满足条件
满足条件 ,试求
,试求 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市高三(上)期末数学试卷(解析版) 题型:解答题
 (q>0是常数).
(q>0是常数). (q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件吗?若是,请给出证明;若不是,请说明理由.
(q>0是常数)”是命题t:“数列{an}是公比为q(q>0)的等比数列”的充要条件吗?若是,请给出证明;若不是,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:
. 给出命题:若![]() 是正常数,且
是正常数,且![]() ,
,![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时等号成立). 根据上面命题,可以得到函数
时等号成立). 根据上面命题,可以得到函数![]() (
(![]() )的k*s#5^u最小值及取最小值时的k*s#5^ux值分
)的k*s#5^u最小值及取最小值时的k*s#5^ux值分![]() 别为( )
别为( )
A.11+6![]()
![]() ,
,![]() B.11+6
B.11+6![]() ,
,![]() C.5,
C.5,![]() D.25,
D.25,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com