
【题目】已知![]() ,
, ![]() .
.
(1)当![]() 时,
时, ![]() 为增函数,求实数
为增函数,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)作差,求导,利用导函数非负恒成立转化为不等式恒成立问题,再分离参数,将问题转化为利用导数研究函数的最值问题;(2)作差构造函数,求导,利用导函数的符号变换确定导数的单调性和最值.
试题解析:(1)∵![]() ,∴
,∴![]() .
.
∵![]() 时
时![]() 为增函数,∴
为增函数,∴![]() 对
对![]() 恒成立,即
恒成立,即![]() .
.
令![]() ,
, ![]() ,则
,则![]() ,令
,令![]() 解得
解得![]() .
.
∴![]() 在
在![]() 单减;
单减; ![]() 单增,∵
单增,∵![]() ,
,
![]() ,∴
,∴![]() .
.
(2)∵![]() 对
对![]() 恒成立,令
恒成立,令![]() 得
得![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
则![]() 在
在![]() 单增,
单增, ![]() 单减;
单减; ![]() ,故
,故![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 单减,∵
单减,∵![]() ,无论
,无论![]() 在
在![]() 有无零点,
有无零点,
![]() 在
在![]() 上的最小值只可能为
上的最小值只可能为![]() 或
或![]() ,
,
要![]() 恒成立,∴
恒成立,∴![]() 且
且![]() ,∴
,∴![]() .
.
法二: ![]() ,即
,即![]() ,令
,令![]() ,
, ![]() ,
,
令![]() 得
得![]() ,∴
,∴![]() 在
在![]() 单增;
单增; ![]() 单减,
单减,
又∵![]() 有唯一零点
有唯一零点![]() ,所以可作出函数
,所以可作出函数![]() 的示意图,
的示意图,
要满足![]() 对
对![]() 恒成立,只需
恒成立,只需 解得
解得![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销量价格P(元)的关系如图所示;③每月需各种开支2 000元.
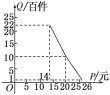
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
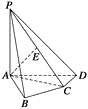
(1) 证明:AE⊥平面PCD;
(2) 求PB和平面PAD所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx为偶函数,数列{an}满足an+1=2f(an-1)+1,且a1=3,an>1.
(1)设bn=log2(an-1),证明:数列{bn+1}为等比数列;
(2)设cn=nbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(1)求证:OC⊥PD;
(2)若PD与平面PAB所成的角为30°,求二面角DPCB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到定点F(1,0)和到直线x=2的距离之比为![]() ,设动点P的轨迹为曲线E,过点F作垂直于x轴的直线与曲线E相交于A,B两点,直线l:y=mx+n与曲线E交于C,D两点,与线段AB相交于一点(与A,B不重合).
,设动点P的轨迹为曲线E,过点F作垂直于x轴的直线与曲线E相交于A,B两点,直线l:y=mx+n与曲线E交于C,D两点,与线段AB相交于一点(与A,B不重合).
(1)求曲线E的方程;
(2)当直线l与圆x2+y2=1相切时,四边形ABCD的面积是否有最大值?若有,求出其最大值及对应的直线l的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+b|≤M;
(2)证明:M≥![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com