练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若x＞1，则函数y=$\frac{{x}^{2}-x+1}{x-1}$的最小值为3．

    分析 换元可得t=x-1＞0，可得x=t+1，代入可得y=t+$\frac{1}{t}$+1，由基本不等式可得．

    解答 解：∵x＞1，∴t=x-1＞0，解得x=t+1，
    ∴y=$\frac{{x}^{2}-x+1}{x-1}$=$\frac{（t+1）^{2}-（t+1）+1}{t}$
    =$\frac{{t}^{2}+t+1}{t}$=t+$\frac{1}{t}$+1≥2$\sqrt{t•\frac{1}{t}}$+1=3，
    当且仅当t=$\frac{1}{t}$即t=1即x=2时取等号．
    故答案为：3．

    点评 本题考查基本不等式求最值，整体换元是解决问题的关键，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

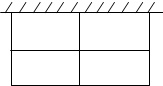    10．如图，动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．现有可围36m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼的面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．二次函数f（x）和g（x）图象开口大小相同，开口方向相反，已知函数g（x）=2x2，f（x）图象的顶点是（1，-7），求：
    （1）f（x）的解析式；
    （2）f（x）在[-2，2]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．以极点为平面直角坐标系的原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程是$\left\{\begin{array}{l}{x=4+tcosa}\\{y=2+tcosa}\end{array}\right.$ （t为参数，a为直线l的倾斜角），曲线C的极坐标方程为ρ=4cosθ
    （1）写出曲线C的直角坐标方程
    （2）直线l与曲线C交于不同的两点M，N，设P（4，2）．求|PM|+|PN|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．函数y=$\frac{x+2}{x+1}$的值域是（-∞，1）∪（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$求：
    （1）z=x2+y2-10y+25的最小值和最大值；
    （2）z=$\frac{y+1}{x+1}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求$\frac{sin50°+cos40°（1+\sqrt{3}tan10°）}{co{s}^{2}20}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在各项均为正数的等比数列{an}中，已知a1+2a2=a3+2a4-1，则a5+2a6的最小值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（　　）
    A．14斛B．22斛C．36斛D．66斛

    查看答案和解析>>

    同步练习册答案