
【题目】如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.

科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 过定点A(1,0).
过定点A(1,0).
(Ⅰ)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(Ⅱ)若![]() 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又![]() 与
与![]() 的交点为N,求证:
的交点为N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知BD为圆锥AO底面的直径,若![]() ,C是圆锥底面所在平面内一点,
,C是圆锥底面所在平面内一点,![]() ,且AC与圆锥底面所成角的正弦值为
,且AC与圆锥底面所成角的正弦值为![]() .
.
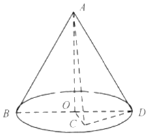
(1)求证:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|,关于x的不等式f(x)<3﹣|2x+1|的解集记为A.
(1)求A;
(2)已知a,b∈A,求证:f(ab)>f(a)﹣f(b).
查看答案和解析>>
科目:高中数学 来源: 题型:
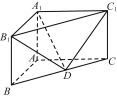
【题目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1) 求直线DC1与平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产某种产品![]() 吨,当日生产的产品当日销售完毕,当
吨,当日生产的产品当日销售完毕,当![]() 时,每日的销售额
时,每日的销售额![]() (单位:万元)与当日的产量
(单位:万元)与当日的产量![]() 满足
满足![]() ,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
,当日产量超过20吨时,销售额只能保持日产量20吨时的状况.已知日产量为2吨时销售额为4.5万元,日产量为4吨时销售额为8万元.
(1)把每日销售额![]() 表示为日产量
表示为日产量![]() 的函数;
的函数;
(2)若每日的生产成本![]() (单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.
(注:计算时取![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学学校对高三年级文科学生进行了一次自主学习习惯的自评满意度的调查,按系统抽样方法得到了一个自评满意度(百分制,单位:分)的样本,如图分别是该样本数据的茎叶图和频率分布直方图(都有部分缺失).
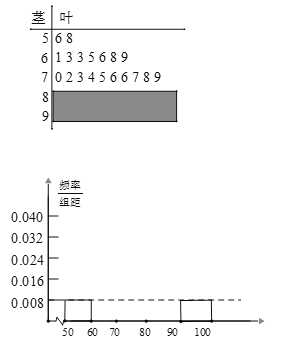
(1)完善频率分布直方图(需写出计算过程);
(2)分别根据茎叶图和频率分布直方图求出样本数据的中位数m1和m2,并指出选用哪一个数据来估计总体的中位数更合理(需要叙述理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com