[题目]一个盒子里装有标号为的张标签.随机的选取两张标签.(1)若标签的选取是无放回的.求两张标签上的数字为相邻整数的概率,(2)若标签的选取是有放回的.求两张标签上的数字至少有一个为5的概率. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】一个盒子里装有标号为的张标签，随机的选取两张标签.

（1）若标签的选取是无放回的，求两张标签上的数字为相邻整数的概率；

（2）若标签的选取是有放回的，求两张标签上的数字至少有一个为5的概率.

【答案】（1）（2）

【解析】

（1）先求出无放回的从5张标签随机地选取两张标签的基本事件总数，再求出两张标签上的数字为相邻整数的基本事件数，从而得到概率；

（2）先求出有放回的从5张标签随机地选取两张标签的基本事件总数，再求出两张标签上的数字至少有一个为5的基本事件数，从而得到概率.

解：（1）由题意知本题是一个等可能事件的概率，无放回的从5张标签随机地选取两张标签的基本事件有个，
两张标签上的数字为相邻整数基本事件有个，
∴根据等可能事件的概率公式得到；

（2）由题意知本题是一个等可能事件的概率，有放无回的从5张标签随机地选取两张标签的基本事件有个，

两张标签上的数字至少有一个为5的基本事件有个，

∴根据等可能事件的概率公式得到.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某书店为了了解销售单价（单位：元）在内的图书销售情况，从2018年上半年已经销售的图书中随机抽取100本，获得的所有样本数据按照，，，，，分成6组，制成如图所示的频率分布直方图，已知样本中销售单价在内的图书数是销售单价在内的图书数的2倍.

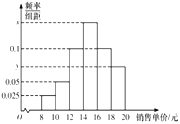
（1）求出x与y，再根据频率分布直方图佔计这100本图书销售单价的平均数、中位数（同一组中的数据用该组区间的中点值作代表）；

（2）用分层抽样的方法从销售单价在内的图书中共抽取40本，求单价在6组样本数据中的图书销售的数量；

（3）从（2）中抽取且价格低于12元的书中任取2本，求这2本书价格都不低于10元的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线x2＝4y的焦点F和点A(－1,8)，点P为抛物线上一点，则|PA|＋|PF|的最小值为(　　)

A. 16 B. 6 C. 12 D. 9

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本万元，且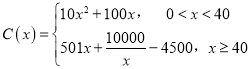．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．

（1）求出2018年的利润L（x）（万元）关于年产量x（百辆）的函数关系式；（利润=销售额-成本）

（2）2018年产量为多少百辆时，企业所获利润最大?并求出最大利润．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知集合，函数定义于并取值于．（用数字作答）

（1）若对于任意的成立，则这样的函数有_______个；

（2）若至少存在一个，使，则这样的函数有____个．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知，函数

讨论的单调性；

若是的极值点，且曲线在两点处的切线相互平行，这两条切线在轴上的截距分别为，求的取值范围

查看答案和解析>>

科目：高中数学 来源： 题型：

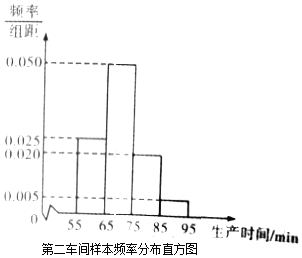
【题目】某工厂有两个车间生产同一种产品，第一车间有工人200人，第二车间有工人400人，为比较两个车间工人的生产效率，采用分层抽样的方法抽取工人，并对他们中每位工人生产完成一件产品的时间（单位：min）分别进行统计，得到下列统计图表（按照[55，65），[65，75），[75，85），[85，95]分组）．