
【题目】已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(Ⅰ)求该几何体的体积V;
(Ⅱ)求该几何体的面积S.
【答案】解:(Ⅰ)由三视图知该几何体是一个底面为矩形,高为4,顶点在底面的射影是底面中心的四棱锥,
∴该几何体的体积V= ![]() =64.
=64.
(Ⅱ)该四棱锥有两个侧面是全等的等腰三角形,且其高为h1= ![]() =4
=4 ![]() ,
,
另外两个侧面也是全等的等腰三角形,这两个侧面的高为 ![]() =
= ![]() =5,
=5,
∴该几何体的面积S=2( ![]() )+8×6=88+24
)+8×6=88+24 ![]() .
.
【解析】(Ⅰ)由三视图知该几何体是一个底面为矩形,高为4,顶点在底面的射影是底面中心的四棱锥,由此能求出该几何体的体积.(Ⅱ)该四棱锥有两个侧面是全等的等腰三角形,另外两个侧面也是全等的等腰三角形,由此能求出该几何体的面积.
【考点精析】掌握由三视图求面积、体积是解答本题的根本,需要知道求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积.


科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= ![]() .
.
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦;
(Ⅲ)求点E到平面ACD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:①f(0)=0,②f(x)+f(1﹣x)=1,③f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )+f(
)+f( ![]() )等于( )
)等于( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.经过空间内的三个点有且只有一个平面
B.如果直线l上有一个点不在平面α内,那么直线上所有点都不在平面α内
C.四棱锥的四个侧面可能都是直角三角形
D.用一个平面截棱锥,得到的几何体一定是一个棱锥和一个棱台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一学生周末的“阅读时间”,从高一年级中随机抽取了![]() 名学生进行调査,获得了每人的周末“阅读时间”(单位:小时),按照
名学生进行调査,获得了每人的周末“阅读时间”(单位:小时),按照![]() 分成
分成![]() 组,制成样本的频率分布直方图如图所示:
组,制成样本的频率分布直方图如图所示:
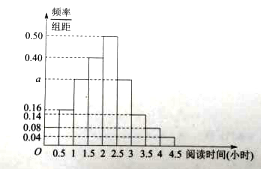
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)估计该校高一学生周末“阅读时间”的中位数;
(Ⅲ)用样本频率代替概率. 现从全校高一年级随机抽取![]() 名学生,其中有
名学生,其中有![]() 名学生“阅读时间”在
名学生“阅读时间”在![]() 小时内的概率为
小时内的概率为![]() ,其中
,其中![]() .当
.当![]() 取最大时,求
取最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x∈R),如图是函数f(x)在[0,+∞)上的图象,
(x∈R),如图是函数f(x)在[0,+∞)上的图象,
(1)求a的值,并补充作出函数f(x)在(﹣∞,0)上的图象,说明作图的理由;
(2)根据图象指出(不必证明)函数的单调区间与值域;
(3)若方程f(x)=lnb恰有两个不等实根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中.

(1)求成绩在区间![]() 内的学生人数及成绩在区间
内的学生人数及成绩在区间![]() 内平均成绩;
内平均成绩;
(2)从成绩大于等于80分的学生中随机选3名学生,求至少有1名学生成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,3m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1)
①求实数a的值;
②设t1= ![]() f(x),t2=g(x),t3=2x , 当x∈(0,1)时,试比较t1 , t2 , t3的大小.
f(x),t2=g(x),t3=2x , 当x∈(0,1)时,试比较t1 , t2 , t3的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com