
【题目】已知函数 .
.
(1)若f(-1)=f(1),求a,并直接写出函数![]() 的单调增区间;
的单调增区间;
(2)当a≥![]() 时,是否存在实数x,使得
时,是否存在实数x,使得![]() =一
=一![]() ?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
【答案】(1)![]() ,单调增区间为
,单调增区间为![]() ,
,![]() ;(2)2个.
;(2)2个.
【解析】
(1)首先根据题中所给的函数解析式,利用![]() ,得到
,得到![]() 所满足的等量关系式,求得
所满足的等量关系式,求得![]() 的值,从而得到函数的解析式,进而求得函数的单调增区间;
的值,从而得到函数的解析式,进而求得函数的单调增区间;
(2)根据条件,结合函数解析式,分类讨论,分析性质,
(1)由![]() ,得
,得![]() ,解得
,解得![]() .
.
此时,函数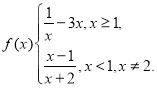
所以函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() .
.
(2)显然,![]() 不满足
不满足![]() ;
;
若![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,
,
化简,得![]() ,无解:
,无解:
若![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,
,
化简,得![]() .
.
令![]() ,
,![]() .
.
当![]() 时,
时,![]() ;
;
下面证明函数![]() 在
在![]() 上是单调增函数.
上是单调增函数.
任取![]() ,且
,且![]() ,
,
则![]()
![]()
由于![]()
![]()
![]()
![]()
![]()
![]() ,
,
所以![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上是单调增函数。
上是单调增函数。
因为![]() ,
,![]() ,
,
所以![]() ,又函数
,又函数![]() 的图象不间断,所以函数
的图象不间断,所以函数![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
即当![]() 时,有且只有一个实数x满足
时,有且只有一个实数x满足![]() .
.
因为当![]() 满足
满足![]() 时,实数
时,实数![]() 也一定满足
也一定满足![]() ,即满足
,即满足![]() 的根成对出现(互为相反数);
的根成对出现(互为相反数);
所以,所有满足![]() 的实数x的个数为2.
的实数x的个数为2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知三点![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() .
.
(1)求![]() 的方程;
的方程;
(2)动点![]()
![]() 在曲线
在曲线![]() 上,
上,![]() 是曲线
是曲线![]() 在
在![]() 处的切线.问:是否存在定点
处的切线.问:是否存在定点![]() 使得
使得![]() 与
与![]() 都相交,交点分别为
都相交,交点分别为![]() ,且
,且![]() 与
与![]() 的面积之比为常数?若存在,求
的面积之比为常数?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣mx(m∈R). (Ⅰ)当m=0时,讨论函数f(x)的单调性;
﹣mx(m∈R). (Ⅰ)当m=0时,讨论函数f(x)的单调性;
(Ⅱ)当b>a>0时,总有 ![]() >1成立,求实数m的取值范围.
>1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为![]() rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=
rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=![]() (OA//BC),则8min后该盛水筒到水面的距离为____m.
(OA//BC),则8min后该盛水筒到水面的距离为____m.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:

(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市从高二年级随机选取1000名学生,统计他们选修物理、化学、生物、政治、历史和地理六门课程(前3门为理科课程,后3门为文科课程)的情况,得到如下统计表,其中“√”表示选课,“空白”表示未选.
方案 人数 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
一 | 220 | √ | √ | √ | |||
二 | 200 | √ | √ | √ | |||
三 | 180 | √ | √ | √ | |||
四 | 175 | √ | √ | √ | |||
五 | 135 | √ | √ | √ | |||
六 | 90 | √ | √ | √ | |||
(Ⅰ)在这1000名学生中,从选修物理的学生中随机选取1人,求该学生选修政治的概率;
(Ⅱ)在这1000名学生中,从选择方案一、二、三的学生中各选取2名学生,如果在这6名学生中随机选取2名,求这2名学生除选修物理以外另外两门选课中有相同科目的概率;
(Ⅲ)利用表中数据估计该市选课偏文(即选修至少两门文科课程)的学生人数多还是偏理(即选修至少两门理科课程)的学生人数多,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“![]() 三个内角的度数可以构成等差数列”是“
三个内角的度数可以构成等差数列”是“![]() 中有一个内角为
中有一个内角为![]() ”的( )
”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() )作为样本(样本容量为
)作为样本(样本容量为![]() )进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生,求所抽取的
名学生,求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com