
| A. | 若l?β且m∥β,则l∥m | B. | 若l⊥m且l⊥n,则m∥n | ||
| C. | 若m⊥n且m?α,n?β,则l∥α | D. | 若m⊥α且m∥n,n∥β,则α⊥β |
分析 在A中,l与m平行或异面;在B中,m与n相交、平行或异面;在C中,l与α相交、平行或l?α;在D中,由面面垂直的判定定理得α⊥β.
解答 解:由l,m,n是三条不同的直线,α,β是两个不同的平面,知:
在A中,若l?β且m∥β,则l与m平行或异面,故A错误;
在B中,若l⊥m且l⊥n,则m与n相交、平行或异面,故B错误;
在C中,若m⊥n且m?α,n?β,则l与α相交、平行或l?α,故C错误;
在D中,若m⊥α且m∥n,n∥β,则由面面垂直的判定定理得α⊥β,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | a | -1 | 1.58 | b | -5.68 | -39.42 | -109.19 | -227 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
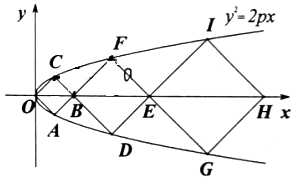 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )| A. | 1:2:3 | B. | 1:4:9 | C. | 2:3:4 | D. | 4:9:16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(cosβ) | B. | f(sinα)<f(cosβ) | C. | f(cosα)<f(cosβ) | D. | f(sinα)>f(sinβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $\frac{16}{3}$ | C. | 32 | D. | 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com