[题目]下列函数中.与函数y=﹣e|x|的奇偶性相同.且在上单调性也相同的是( )A.B.y=ln|x|C.y=x3﹣3D.y=﹣x2+2 题目和参考答案——青夏教育精英家教网—

【题目】下列函数中，与函数y=﹣e|x|的奇偶性相同，且在（﹣∞，0）上单调性也相同的是（）
A.
B.y=ln|x|
C.y=x3﹣3
D.y=﹣x2+2

【答案】D
【解析】解：函数y=﹣e|x|为偶函数，且在（﹣∞，0）上单调递增．A. 为奇函数，不满足条件．
B．y=ln|x|为偶函数，当x＜0时，函数为y=ln（﹣x）单调递减．不满足条件．
C．y=x3﹣3为非奇非偶函数，不满足条件．
D．y=﹣x2+2为偶函数，在（﹣∞，0）上单调递增，满足条件．
故选：D
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点，需要掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题．

练习册系列答案

步步高练加测系列答案

汇练系列答案

快乐假期暑假作业新疆人民出版社系列答案

快乐暑假假期作业云南人民出版社系列答案

英语小英雄天天默写系列答案

英才园地系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】近年来，手机已经成为人们日常生活中不可缺少的产品，手机的功能也日趋完善，已延伸到了各个领域，如拍照，聊天，阅读，缴费，购物，理财，娱乐，办公等等，手机的价格差距也很大，为分析人们购买手机的消费情况，现对某小区随机抽取了200人进行手机价格的调查，统计如下：

年龄价格	5000元及以上	3000元﹣4999元	1000元﹣2999元	1000元以下
45岁及以下	12	28	66	4
45岁以上	3	17	46	24

（Ⅰ）完成关于人们使用手机的价格和年龄的2×2列联表，再判断能否在犯错误的概率不超过0.025的前提下，认为人们使用手机的价格和年龄有关？
（Ⅱ）从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况，设3人中年龄在45岁及以下的人数为随机变量X，求随机变量X的分布列及数学期望．
附K2=

P（K2≥k）	0.05	0.025	0.010	0.001
k	3.841	5.024	6.635	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．（Ⅰ）求C；
（Ⅱ）若c= ，△ABC的面积为，求△ABC的周长．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，直线l的参数方程为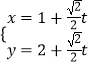（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为ρ=6sinθ．（Ⅰ）求直角坐标下圆C的标准方程；
（Ⅱ）若点P（l，2），设圆C与直线l交于点A，B，求|PA|+|PB|的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=cos（x+ ）+sinx．
（I）利用“五点法”，列表并画出f（x）在[﹣ ， ]上的图象；
（II）a，b，c分别是△ABC中角A，B，C的对边．若a= ，f（A）= ，b=1，求△ABC的面积．


x
f（x）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于函数f（x）= ，有下列5个结论：
①任取x1 ， x2∈[0，+∞），都有|f（x1）﹣f（x2）|≤2；
②函数y=f（x）在区间[4，5]上单调递增；
③f（x）=2kf（x+2k）（k∈N+），对一切x∈[0，+∞）恒成立；
④函数y=f（x）﹣ln（x﹣1）有3个零点；
⑤若关于x的方程f（x）=m（m＜0）有且只有两个不同实根x1 ， x2 ，则x1+x2=3．
则其中所有正确结论的序号是．（请写出全部正确结论的序号）