已知f(x)=x2+C,且f[f(x)]=f(x2+1)
(1)设g(x)=f[(x)],求g(x)的解析式.
(2)设?(x)=g(x)-λf(x),试问是否存在实数λ,使?(x)在(-∞,-1)上是减函数,并且在(-1,0)上是增函数.
解:(1)由题意可知:
f(x)=x
2+C,且f[f(x)]=f(x
2+1)
∴(x
2+c)
2+c=(x
2+1)
2+c
∴x
4+2cx
2+c
2=x
4+2x
2+1
∴
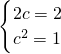
,解得:c=1.
∴f(x)=x
2+1,∵g(x)=f[(x)],
∴函数g(x)的解析式为:g(x)=x
4+2x
2+2.
(2)由(1)可知:f(x)=x
2+1、g(x)=x
4+2x
2+2,
∵?(x)=g(x)-λf(x),
∴θ(x)=x
4+(2-λ)x
2+2-λ,∴θ′(x)=4x
3+2(2-λ)x
假设存在使的?(x)在(-∞,-1)上是减函数,并且在(-1,0)上是增函数.
则θ′(-1)=0
∴-4-2(2-λ)=0,∴λ=4.
此时:θ(x)=x
4-2x
2-2,∴θ′(x)=4x
3-4x.
由θ′(x)>0解得,x∈(-1,0)∪(1,+∞);
由θ′(x)<0解得,x∈(-∞,-1)∪(0,1).
故满足题意.
所以存在λ=4使的?(x)在(-∞,-1)上是减函数,并且在(-1,0)上是增函数.
分析:(1)结合条件充分利用复合函数内函数的值域是外函数的定义域的特点整体代入,进而即可获得一个多项式方程,利用对应系数相等即可获得问题的解答;
(2)利用第一问的结论即可化简函数?(x)=g(x)-λf(x),得:θ(x)=x
4+(2-λ)x
2+2-λ,又因为实数λ,使?(x)在(-∞,-1)上是减函数,并且在(-1,0)上是增函数,所以导函数在-1处的函数值为零进而求得参数λ,注意最后验证即可.
点评:本题考查的是函数解析式的求法及恒成立知识的综合类问题.在解答的过程当中充分体现了复合函数的知识、对应系数相等的技巧、导数的知识以及恒成立问题的解答规律.值得同学们体会和反思.

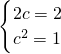 ,解得:c=1.
,解得:c=1.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案