
【题目】我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( ) 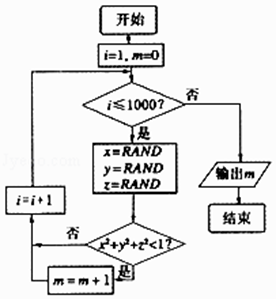
A.3.119
B.3.126
C.3.132
D.3.151
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的第2项、第5项分别为二项式(2x+1)5展开式的第5项、第2项的系数.
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn , 若存在实数λ,使 ![]() 恒成立,求实数λ的取值范围.
恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市![]() 岁的人群抽取一个容量为
岁的人群抽取一个容量为![]() 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
,再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样方法抽取
组回答正确的人中用分层抽样方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求:所抽取的人中第2组至少有
人颁发幸运奖,求:所抽取的人中第2组至少有![]() 人获得幸运奖概率.
人获得幸运奖概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(sinx+cosx).
(1)如果对于任意的x∈[0, ![]() ],f(x)≥kx+excosx恒成立,求实数k的取值范围;
],f(x)≥kx+excosx恒成立,求实数k的取值范围;
(2)若x∈[﹣ ![]() ,
, ![]() ],过点M(
],过点M( ![]() ,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和.
,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() ,过点
,过点 ![]() 的直线
的直线 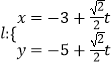 (
( ![]() 为参数)与曲线
为参数)与曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() 两点.
两点.
(1)求曲线 ![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线 ![]() 的普通方程;
的普通方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过圆
过圆![]() 与直线
与直线![]() 的交点,且圆
的交点,且圆![]() 上任意一点关于直线
上任意一点关于直线![]() 的对称点仍在圆
的对称点仍在圆![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点(异于点
两点(异于点![]() ),且点
),且点![]() 满足
满足![]() ,
,![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)求函数f(x)的单调区间;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() ;
;
(3)设h(x)=f(x+1)+g(x),当x≥0,h(x)≥1时,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com