
ЁОЬтФПЁПДгФГЙЄГЇЕФвЛИіГЕМфГщШЁФГжжВњЦЗ50МўЃЌВњЦЗГпДчЃЈЕЅЮЛЃКcmЃЉТфдкИїИіаЁзщЕФЦЕЪ§ЗжВМШчЯТБэЃК
Ъ§ОнЗжзщ | [12.5ЃЌ15.5ЃЉ | [15.5ЃЌ18.5ЃЉ | [18.5ЃЌ21.5ЃЉ | [21.5ЃЌ24.5ЃЉ | [24.5ЃЌ27.5ЃЉ | [27.5ЃЌ30.5ЃЉ | [30.5ЃЌ33.5ЃЉ |
ЦЕЪ§ | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
ЃЈ1ЃЉИљОнЦЕЪ§ЗжВМБэЃЌЧѓИУВњЦЗГпДчТфдк[27.5ЃЌ33.5]ФкЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓет50МўВњЦЗГпДчЕФбљБОЦНОљЪ§![]() ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉЃЛ
ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉЃЛ
ЃЈ3ЃЉИљОнЦЕЪ§ЗжВМЖдгІЕФжБЗНЭМЃЌПЩвдШЯЮЊетжжВњЦЗГпДч![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌЦфжа
ЃЌЦфжа![]() НќЫЦЮЊбљБОЦНОљжЕ
НќЫЦЮЊбљБОЦНОљжЕ![]() ЃЌ
ЃЌ![]() НќЫЦЮЊбљБОЗНВю
НќЫЦЮЊбљБОЗНВю![]() ЃЌОМЦЫуЕУ
ЃЌОМЦЫуЕУ![]() .РћгУИУе§ЬЌЗжВМЃЌЧѓ
.РћгУИУе§ЬЌЗжВМЃЌЧѓ![]() ЃЈ
ЃЈ![]() ЃЉ.
ЃЉ.
ИНЃКЃЈ1ЃЉШєЫцЛњБфСП![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌдђ
ЃЌдђ![]()
![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ0.16ЃЛЃЈ2ЃЉ22.7ЃЛЃЈ3ЃЉ0.1587
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгИљОнЦЕЪ§ЗжВМБэЧѓГпДчТфдк[27.5ЃЌ33.5ЃЉФкЕФИХТЪЃЛ
ЃЈ2ЃЉгЩУПвЛзщЪ§ОнЕФжаМфжЕГЫвдЦЕТЪзїКЭЧѓЕУбљБОЦНОљЪ§ЃЛ
ЃЈ3ЃЉвРЬтвт![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() гы
гы![]() ЃЌдйгЩе§ЬЌЗжВМЧњЯпЕФЖдГЦадЧѓPЃЈzЁн27.43ЃЉЃН0.1587ЃЎ
ЃЌдйгЩе§ЬЌЗжВМЧњЯпЕФЖдГЦадЧѓPЃЈzЁн27.43ЃЉЃН0.1587ЃЎ
ЃЈ1ЃЉИљОнЦЕЪ§ЗжВМБэПЩжЊЃЌВњЦЗГпДчТфдк[27.5,33.5]ФкЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉбљБОЦНОљЪ§![]()
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉвРЬтвт![]() ЃЌЖј
ЃЌЖј![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЖдШЮвтЕФ
ЖдШЮвтЕФ![]() ЖМга
ЖМга![]() ЃЌЧв
ЃЌЧв![]() ЪБ
ЪБ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌЯТСаЫФИіНсТлЃКЂй
ЃЌЯТСаЫФИіНсТлЃКЂй![]() ЪЧ
ЪЧ![]() ЕФвЛИіМЋжЕЕуЃЛЂкШє
ЕФвЛИіМЋжЕЕуЃЛЂкШє![]() ЮЊЦцКЏЪ§ЃЌдђ
ЮЊЦцКЏЪ§ЃЌдђ![]() ЕФзюаЁе§жмЦк
ЕФзюаЁе§жмЦк![]() ЃЛЂлШє
ЃЛЂлШє![]() ЮЊХМКЏЪ§ЃЌдђ
ЮЊХМКЏЪ§ЃЌдђ![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЛЂм
ЩЯЕЅЕїЕндіЃЛЂм![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() .ЦфжавЛЖЈе§ШЗЕФНсТлБрКХЪЧЃЈ ЃЉ
.ЦфжавЛЖЈе§ШЗЕФНсТлБрКХЪЧЃЈ ЃЉ
A.ЂйЂкB.ЂйЂлC.ЂйЂкЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕХњСПЩњВњСЫвЛжжЦћГЕХфМўЃЌзмЪ§ЮЊ![]() ЃЌХфМўАќзАЩЯБъгаДг1ЕН
ЃЌХфМўАќзАЩЯБъгаДг1ЕН![]() ЕФСЌајздШЛЪ§ађКХЃЌЮЊЖдХфМўзмЪ§
ЕФСЌајздШЛЪ§ађКХЃЌЮЊЖдХфМўзмЪ§![]() НјааЙРМЦЃЌжЪМьдБЫцЛњГщШЁСЫ
НјааЙРМЦЃЌжЪМьдБЫцЛњГщШЁСЫ![]() ИіХфМўЃЌађКХДгаЁЕНДѓвРДЮЮЊ
ИіХфМўЃЌађКХДгаЁЕНДѓвРДЮЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌет
ЃЌет![]() ИіађКХЯрЕБгкДгЧјМф
ИіађКХЯрЕБгкДгЧјМф![]() ЩЯЫцЛњГщШЁСЫ
ЩЯЫцЛњГщШЁСЫ![]() ИіећЪ§ЃЌет
ИіећЪ§ЃЌет![]() ИіећЪ§НЋЧјМф
ИіећЪ§НЋЧјМф![]() ЗжЮЊ
ЗжЮЊ![]() ИіаЁЧјМф
ИіаЁЧјМф![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЎгЩгкет
ЃЎгЩгкет![]() ИіећЪ§ЪЧЫцЛњГщШЁЕФЃЌЫљвдЧА
ИіећЪ§ЪЧЫцЛњГщШЁЕФЃЌЫљвдЧА![]() ИіЧјМфЕФЦНОљГЄЖШ
ИіЧјМфЕФЦНОљГЄЖШ![]() гыЫљга
гыЫљга![]() ИіЧјМфЕФЦНОљГЄЖШ
ИіЧјМфЕФЦНОљГЄЖШ![]() НќЫЦЯрЕШЃЌНјЖјПЩвдЕУЕН
НќЫЦЯрЕШЃЌНјЖјПЩвдЕУЕН![]() ЕФЙРМЦжЕЃЎвбжЊ
ЕФЙРМЦжЕЃЎвбжЊ![]() ЃЌжЪМьдБЫцЛњГщШЁЕФХфМўађКХДгаЁЕНДѓвРДЮЮЊ83ЃЌ135ЃЌ274ЃЌЁЃЌ3104ЃЎ
ЃЌжЪМьдБЫцЛњГщШЁЕФХфМўађКХДгаЁЕНДѓвРДЮЮЊ83ЃЌ135ЃЌ274ЃЌЁЃЌ3104ЃЎ
ЃЈ1ЃЉгУЩЯУцЕФЗНЗЈЧѓ![]() ЕФЙРМЦжЕЃЎ
ЕФЙРМЦжЕЃЎ
ЃЈ2ЃЉНЋЃЈ1ЃЉжаЕФ![]() ЙРМЦжЕзїЮЊетХњЦћГЕХфМўЕФзмЪ§ЃЌДгжаЫцЛњГщШЁ100ИіХфМўВтСПЦфФкОЖ
ЙРМЦжЕзїЮЊетХњЦћГЕХфМўЕФзмЪ§ЃЌДгжаЫцЛњГщШЁ100ИіХфМўВтСПЦфФкОЖ![]() ЃЈЕЅЮЛЃК
ЃЈЕЅЮЛЃК![]() ЃЉЃЌЛцжЦГіЦЕТЪЗжВМжБЗНЭМШчЯТЃК
ЃЉЃЌЛцжЦГіЦЕТЪЗжВМжБЗНЭМШчЯТЃК
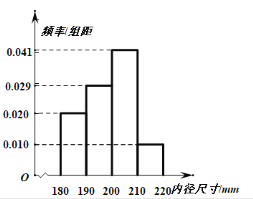
НЋет100ИіХфМўЕФФкОЖТфШыИїзщЕФЦЕТЪЪгЮЊет![]() ИіХфМўФкОЖЗжВМЕФИХТЪЃЌвбжЊБъзМХфМўЕФФкОЖЮЊ200
ИіХфМўФкОЖЗжВМЕФИХТЪЃЌвбжЊБъзМХфМўЕФФкОЖЮЊ200![]() ЃЌАбет
ЃЌАбет![]() ИіХфМўжаФкОЖГЄЖШзюНгНќБъзМХфМўФкОЖГЄЖШЕФ800ИіХфМўЖЈвхЮЊгХЕШЦЗЃЌЧѓгХЕШЦЗХфМўФкОЖ
ИіХфМўжаФкОЖГЄЖШзюНгНќБъзМХфМўФкОЖГЄЖШЕФ800ИіХфМўЖЈвхЮЊгХЕШЦЗЃЌЧѓгХЕШЦЗХфМўФкОЖ![]() ЕФШЁжЕЗЖЮЇЃЈНсЙћБЃСєећЪ§ЃЉЃЎ
ЕФШЁжЕЗЖЮЇЃЈНсЙћБЃСєећЪ§ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕЮЊШЗЖЈЯТвЛФъЭЖШыФГжжВњЦЗЕФбаЗЂЗбгУЃЌашСЫНтФъбаЗЂЗбгУ![]() ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉЖдФъЯњЪлСП
ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉЖдФъЯњЪлСП![]() ЃЈЕЅЮЛЃКЧЇЭђМўЃЉЕФгАЯьЃЌЭГМЦСЫНќ
ЃЈЕЅЮЛЃКЧЇЭђМўЃЉЕФгАЯьЃЌЭГМЦСЫНќ![]() ФъЭЖШыЕФФъбаЗЂЗбгУ
ФъЭЖШыЕФФъбаЗЂЗбгУ![]() гыФъЯњЪлСП
гыФъЯњЪлСП![]() ЕФЪ§ОнЃЌЕУЕНЩЂЕуЭМШчЭМЫљЪОЃЎ
ЕФЪ§ОнЃЌЕУЕНЩЂЕуЭМШчЭМЫљЪОЃЎ
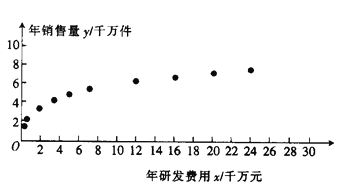
(1)РћгУЩЂЕуЭМХаЖЯ![]() КЭ
КЭ![]() ЃЈЦфжа
ЃЈЦфжа![]() ОљЮЊДѓгк
ОљЮЊДѓгк![]() ЕФГЃЪ§ЃЉФФвЛИіИќЪЪКЯзїЮЊФъЯњЪлСП
ЕФГЃЪ§ЃЉФФвЛИіИќЪЪКЯзїЮЊФъЯњЪлСП![]() КЭФъбаЗЂЗбгУ
КЭФъбаЗЂЗбгУ![]() ЕФЛиЙщЗНГЬРраЭЃЈжЛвЊИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
ЕФЛиЙщЗНГЬРраЭЃЈжЛвЊИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
(2)ЖдЪ§ОнзїГіШчЯТДІРэЃЌСю![]() ЃЌЕУЕНЯрЙиЭГМЦСПЕФжЕШчЯТБэЃКИљОнЕк(1)ЮЪЕФХаЖЯНсЙћМАБэжаЪ§ОнЃЌЧѓ
ЃЌЕУЕНЯрЙиЭГМЦСПЕФжЕШчЯТБэЃКИљОнЕк(1)ЮЪЕФХаЖЯНсЙћМАБэжаЪ§ОнЃЌЧѓ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЃЛ
ЕФЛиЙщЗНГЬЃЛ
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)вбжЊЦѓвЕФъРћШѓ![]() ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉгы
ЃЈЕЅЮЛЃКЧЇЭђдЊЃЉгыЕФЙиЯЕЮЊ
![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌИљОнЕк(2)ЮЪЕФНсЙћХаЖЯЃЌвЊЪЙЕУИУЦѓвЕЯТвЛФъЕФФъРћШѓзюДѓЃЌдЄМЦЯТвЛФъгІЭЖШыЖрЩйбаЗЂЗбгУ?
ЃЉЃЌИљОнЕк(2)ЮЪЕФНсЙћХаЖЯЃЌвЊЪЙЕУИУЦѓвЕЯТвЛФъЕФФъРћШѓзюДѓЃЌдЄМЦЯТвЛФъгІЭЖШыЖрЩйбаЗЂЗбгУ?
ИНЃКЖдгквЛзщЪ§Он![]() ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ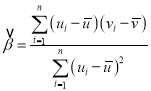 ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈ1ЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() дк
дк![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() дкЖЈвхгђЩЯЧЁгаСНИіВЛЭЌЕФСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
дкЖЈвхгђЩЯЧЁгаСНИіВЛЭЌЕФСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшКЏЪ§![]() дкЧјМф
дкЧјМф![]() )ЩЯДцдкМЋжЕЃЌЧѓжЄЃК
)ЩЯДцдкМЋжЕЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЭМЯѓдк
ЭМЯѓдк![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉШєВЛЕШЪН![]() Жд
Жд![]() КуГЩСЂЃЌЧѓећЪ§
КуГЩСЂЃЌЧѓећЪ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊFЪЧХзЮяЯпCЃКx2ЃН4yЕФНЙЕуЃЌЙ§EЃЈ0ЃЌЉ1ЃЉЕФжБЯпlгыХзЮяЯпЗжeНЛгкAЃЌBСНЕуЃЎ
ЃЈ1ЃЉЩшжБЯпAFЃЌBFЕФаБТЪЗжeЮЊk1ЃЌk2ЃЌжЄУїЃКk1+k2ЃН0ЃЛ
ЃЈ2ЃЉШє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЮЊЕШВюЪ§СаЃЌИїЯюЮЊе§ЕФЕШБШЪ§Са
ЮЊЕШВюЪ§СаЃЌИїЯюЮЊе§ЕФЕШБШЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ__________.дкЂй
ЃЌ__________.дкЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() етШ§ИіЬѕМўжаШЮбЁЦфжавЛИіЃЌВЙГфдкКсЯпЩЯЃЌВЂЭъГЩЯТУцЮЪЬтЕФНтД№ЃЈШчЙћбЁдёЖрИіЬѕМўНтД№ЃЌдђвдбЁдёЕквЛИіНтД№МЧЗжЃЉ.
етШ§ИіЬѕМўжаШЮбЁЦфжавЛИіЃЌВЙГфдкКсЯпЩЯЃЌВЂЭъГЩЯТУцЮЪЬтЕФНтД№ЃЈШчЙћбЁдёЖрИіЬѕМўНтД№ЃЌдђвдбЁдёЕквЛИіНтД№МЧЗжЃЉ.
ЃЈ1ЃЉЧѓЪ§Са![]() КЭ
КЭ![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЧѓЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭ
ЯюКЭ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯжНЋГЄЗНаЮбиЖдНЧЯп
ЃЌЯжНЋГЄЗНаЮбиЖдНЧЯп![]() елЦ№ЃЌЪЙ
елЦ№ЃЌЪЙ![]() ЃЌЕУЕНвЛИіЫФУцЬх
ЃЌЕУЕНвЛИіЫФУцЬх![]() ЃЌШчЭМЫљЪО.
ЃЌШчЭМЫљЪО.
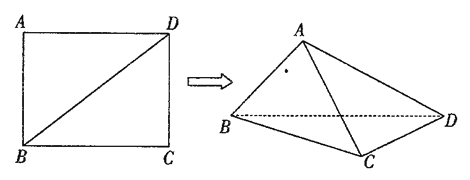
ЃЈ1ЃЉЪдЮЪЃКдкелЕўЕФЙ§ГЬжаЃЌвьУцжБЯп![]() гы
гы![]() ФмЗёДЙжБЃПШєФмДЙжБЃЌЧѓГіЯргІЕФ
ФмЗёДЙжБЃПШєФмДЙжБЃЌЧѓГіЯргІЕФ![]() ЕФжЕЃЛШєВЛДЙжБЃЌЧыЫЕУїРэгЩЃЛ
ЕФжЕЃЛШєВЛДЙжБЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБЫФУцЬх![]() ЬхЛ§зюДѓЪБЃЌЧѓЖўУцНЧ
ЬхЛ§зюДѓЪБЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com