
 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2. 解:(1)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2
解:(1)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2 ,
, ),E(0,4,0)
),E(0,4,0) =(3,0,0),
=(3,0,0),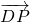 =(0,3,
=(0,3, ),
),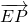 =(0,-1,
=(0,-1, ).∵
).∵ •
•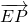 =0,
=0,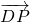 •
•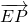 =0,∴
=0,∴ ⊥
⊥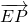 ,
,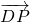 ⊥
⊥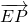 ∴DA⊥EP,DP⊥EP,∵DA,DP是平面ADP内的相交直线,∴PE⊥平面APD.
∴DA⊥EP,DP⊥EP,∵DA,DP是平面ADP内的相交直线,∴PE⊥平面APD. ),E(0,4,0),F(
),E(0,4,0),F( ,4,0),B(3,2,0),∴
,4,0),B(3,2,0),∴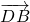 =(3,2,0),
=(3,2,0), =(
=( ,1,-
,1,- )
)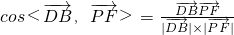 =
=
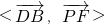 ,∴
,∴
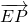 =(0,-1,
=(0,-1, ).
). =(
=( ,1,-
,1,- )
) =
=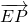 =(0,-1,
=(0,-1, ).
).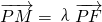 ∴
∴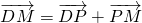 ═(0,3,
═(0,3, )+λ(
)+λ( ,1,-
,1,- )=(
)=( ,λ+3,
,λ+3, )
)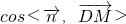 =
=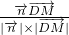 =
=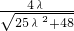 ,如果直线DM与平面ADC所成的角为30°,
,如果直线DM与平面ADC所成的角为30°,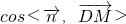 |=sin30°,即
|=sin30°,即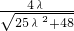 =
= 解得
解得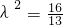


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
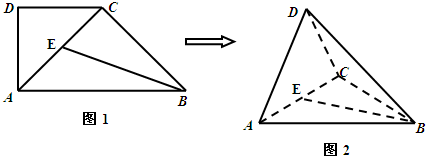 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;查看答案和解析>>
科目:高中数学 来源: 题型:
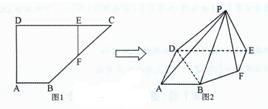 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com