
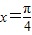 ”是“函数y=sin2x取得最大值”的( )
”是“函数y=sin2x取得最大值”的( )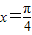 ”⇒“函数y=sin2x取得最大值”与“函数y=sin2x取得最大值”⇒“
”⇒“函数y=sin2x取得最大值”与“函数y=sin2x取得最大值”⇒“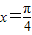 ”的真假,进而根据充要条件的定义即可得到答案.
”的真假,进而根据充要条件的定义即可得到答案.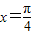 ”时,“函数y=sin2x取得最大值”成立;
”时,“函数y=sin2x取得最大值”成立;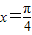 ”是“函数y=sin2x取得最大值”的充分条件,
”是“函数y=sin2x取得最大值”的充分条件,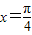 ”不一定成立;
”不一定成立;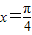 ”是“函数y=sin2x取得最大值”的不必要条件;
”是“函数y=sin2x取得最大值”的不必要条件;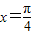 ”是“函数y=sin2x取得最大值”的充分不必要条件
”是“函数y=sin2x取得最大值”的充分不必要条件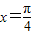 ”⇒“函数y=sin2x取得最大值”与“函数y=sin2x取得最大值”⇒“
”⇒“函数y=sin2x取得最大值”与“函数y=sin2x取得最大值”⇒“ ”的真假是解答本题的关键.
”的真假是解答本题的关键. 

科目:高中数学 来源: 题型:
| 3 |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AO |
| OB |
| OP |
| OA |
| OB |
| PA |
| PB |
| ∫ | 1 0 |
| 1-x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-2x |
| x2-5x+4 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| ∫ | 1 0 |
| 1-x2 |
| OA |
| OB |
| OP |
| OA |
| OB |
| PA |
| PB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com