
【题目】某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为![]() 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
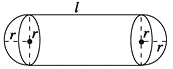
①写出y关于r的函数表达式,并求该函数的定义域;
②求该容器的建造费用最小时的r.
【答案】①y=4π(c-2)r2+![]() ,0<r≤2②当3<c≤
,0<r≤2②当3<c≤![]() 时,建造费用最小时r=2;当c>
时,建造费用最小时r=2;当c>![]() 时,建造费用最小时,r=
时,建造费用最小时,r=![]() .
.
【解析】(1)由体积V=![]() ,解得l=
,解得l=![]() ,
,
∴y=2πrl×3+4πr2×c
=6πr×![]() +4cπr2
+4cπr2
=2π![]() ,
,
又l≥2r,即![]() ≥2r,解得0<r≤2
≥2r,解得0<r≤2
∴其定义域为(0,2].
(2)由(1)得,y′=8π(c﹣2)r﹣![]() ,
,
=![]() ,0<r≤2
,0<r≤2
由于c>3,所以c﹣2>0
当r3﹣![]() =0时,则r=
=0时,则r=![]()
令![]() =m,(m>0)
=m,(m>0)
所以y′=![]()
①当0<m<2即c>![]() 时,
时,
当r=m时,y′=0
当r∈(0,m)时,y′<0
当r∈(m,2)时,y′>0
所以r=m是函数y的极小值点,也是最小值点.
②当m≥2即3<c≤![]() 时,
时,
当r∈(0,2)时,y′<0,函数单调递减.
所以r=2是函数y的最小值点.
综上所述,当3<c≤![]() 时,建造费用最小时r=2;
时,建造费用最小时r=2;
当c>![]() 时,建造费用最小时r=
时,建造费用最小时r=![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,称
,称![]() 为
为![]() 的第
的第![]() 个坐标分量.若
个坐标分量.若![]() ,且满足如下两条性质:
,且满足如下两条性质:
①![]() 中元素个数不少于
中元素个数不少于![]() 个.
个.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 个坐标分量都是
个坐标分量都是![]() .则称
.则称![]() 为
为![]() 的一个好子集.
的一个好子集.
(![]() )若
)若![]() 为
为![]() 的一个好子集,且
的一个好子集,且![]() ,
,![]() ,写出
,写出![]() ,
,![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集,求证:
的一个好子集,求证:![]() 中元素个数不超过
中元素个数不超过![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集且
的一个好子集且![]() 中恰好有
中恰好有![]() 个元素,求证:一定存在唯一一个
个元素,求证:一定存在唯一一个![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 个坐标分量都是
个坐标分量都是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
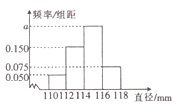
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
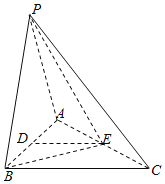
(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求三棱锥P﹣BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
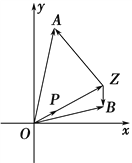
【题目】如图,已知![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点.
(1)求使![]() 取最小值时的
取最小值时的![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
(1)估计这次考试成绩的众数,中位数,平均数;
(2)估计这次考试成绩的及格率(60分及其以上为及格).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在超级计算机方面发展迅速,跻身国际先进水平国家,预报天气的准确度也大大提高,天气预报说今后的三天中,每一天下雨的概率都是![]() ,我们可以通过随机模拟的方法估计概率.我们先产生
,我们可以通过随机模拟的方法估计概率.我们先产生![]() 组随机数
组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用![]() 表示下雨,
表示下雨,![]() 表示不下雨,那么今后的三天中都下雨的概率近似为( )
表示不下雨,那么今后的三天中都下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com